时间:2016-03-06 19:38:53
2011年全国硕士研究生入学统一考试
数学(一)试卷
一、选择题(1-8小题,每小题4分,共32分,下列每小题给出的四个选项中,只有一项符合题目要求,把所选项前的字母填在题后的括号内.)
1、 曲线![]() 的拐点是( )
的拐点是( )
A (1,0) B (2,0) C (3![]() ,0) D (4,0)
,0) D (4,0)
2、设数列![]() 单调减少,且
单调减少,且![]() 。
。![]() 无界,则幂级数
无界,则幂级数![]() 的收敛域为( )
的收敛域为( )
A ![]() B
B ![]() C
C ![]() D
D ![]()
3、 设函数![]() 具有二阶连续的导数,且
具有二阶连续的导数,且![]() .
.![]() 。则函数
。则函数![]() 在点
在点![]() 处取得极小值的一个充分条件是( )
处取得极小值的一个充分条件是( )
A ![]() B
B ![]()
C ![]() D
D ![]()
4、设![]()
![]()
![]() ,则
,则 ![]() 的大小关系是( )
的大小关系是( )
A ![]() B
B ![]() C
C ![]() D
D ![]()
5、设A为3阶矩阵,把A的第二列加到第一列得到矩阵B ,再交换B的第二行与第3行得到单位阵E,记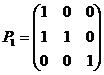 ,
,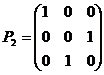 ,则A=( )
,则A=( )
A ![]() B
B ![]() C
C ![]() D
D ![]()
6、设![]() 是4阶矩阵,
是4阶矩阵,![]() 为A的伴随矩阵。若
为A的伴随矩阵。若![]() 是
是![]() 的一个基础解系,则
的一个基础解系,则![]() 的基础解系可为( )
的基础解系可为( )
A ![]() B
B ![]() C
C ![]() D
D ![]()
7、设![]() 为两个分布函数,且连续函数
为两个分布函数,且连续函数![]() 为相应的概率密度,则必为概率密度的是( )
为相应的概率密度,则必为概率密度的是( )
A ![]() B
B ![]() C
C ![]() D
D ![]() +
+![]()
8、设随机变量![]() 相互独立,且
相互独立,且![]() 都存在,记
都存在,记![]()
![]() ,则
,则![]() ( )
( )
A ![]() B
B ![]() C
C ![]() D
D ![]()
二、填空题:9—14小题,每小题4分,共24分,请将答案写在答题纸指定的位置上。
9、曲线![]() 的弧长为_____________
的弧长为_____________
10、微分方程![]() 满足条件
满足条件![]() 的解为________________
的解为________________
11、设函数![]() ,则
,则![]()
12、设![]() 是柱面方程
是柱面方程![]() 与平面
与平面![]() 的交线,从
的交线,从![]() 轴正向往
轴正向往![]() 轴负向看去为逆时针方向,则曲线积分
轴负向看去为逆时针方向,则曲线积分![]()
13、若二次曲面的方程![]() ,经正交变换化为
,经正交变换化为![]() ,则
,则![]()
14、设二维随机变量![]() ,则
,则![]()
三、解答题:15—23小题,共94分.请将解答写在答题纸指定的位置上,解答应写出文字说明,证明过程或演算步骤。
15、(本题满分10分) 求极限![]()
16、(本题满分9分)
设函数![]() ,其中
,其中![]() 具有二阶连续的偏导数,函数
具有二阶连续的偏导数,函数![]() 可导且在
可导且在![]() 处取得极值
处取得极值![]() .求
.求![]()
17、(本题满分10分)
求方程![]() 的不同实根的个数,其中
的不同实根的个数,其中![]() 为参数。
为参数。
18、(本题满分10分)
①证明:对任意的正整数![]() ,都有
,都有![]() 成立;
成立;
②设![]() ,证明数列
,证明数列![]() 收敛.
收敛.
19、(本题满分11分)
已知函数![]() 具有二阶连续的偏导数,且
具有二阶连续的偏导数,且![]() ,其中
,其中![]() 计算二重积分
计算二重积分![]()
20、(本题满分11分)
设向量组![]() ,
,![]() ,
,![]() 不能由向量组
不能由向量组![]() ,
,![]() ,
,![]() 线性表示;
线性表示;
(1) 求![]() 的值;
的值;
(2) 将![]() 用
用![]() 线性表示;
线性表示;
21、(本题满分11分)
A为3阶实对称矩阵,A的秩为2,且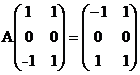
求(1)A的特征值与特征向量 (2) 矩阵A
22、(本题满分11分)
设随机变量X与Y的概率分布分别为
|
X |
0 |
1 |
|
|
|
|
|
Y |
-1 |
0 |
1 |
|
|
|
|
|
且![]()
求(1)二维随机变量(X,Y)的概率分布;
(2)![]() 的概率分布
的概率分布
(3)X与Y的相关系数![]()
23、(本题满分11分)
设![]() 是来自正态总体
是来自正态总体![]() 的简单随机样本,其中
的简单随机样本,其中![]() 已知,
已知,![]() 未知.
未知.![]() 为样本均值和样本方差.
为样本均值和样本方差.
求(1)求参数![]() 的最大似然估计
的最大似然估计![]()
(2) 计算E![]() 和D
和D![]()
2011年全国硕士研究生入学统一考试 数学一试题 答案速查: 一、选择题 (1) (2) (3) (4) (5) (6) (7) (8) C C A B D D D B 二、填空题 (9) (10) (11) (12) (13) (14) 4 1 三、解答题 (15) (16) (17)当 (18)略 (19) (20)(I) (21)(I) (22)(I) (II)
(III) (23)(Ⅰ) 一、选择题:1~8小题,每小题4分,共32分,下列每题给出的四个选项中,只有一个选项符合题目要求,请将所选项前的字母填在答题纸指定位置上. (1) 曲线 (A) 【答案】(C) 【考点】函数图形的拐点 【难易度】★★ 【详解】 解析:由 (2) 设数列 (A) 【答案】(C) 【考点】莱布尼茨定理;幂级数的收敛区间和收敛域 【难易度】★★★ 【详解】 解析: 因此,幂级数 (3) 设函数 (A) (C) 【答案】(A) 【考点】多元函数的极值 【难易度】★★★ 【详解】 解析:由 所以 要使得函数 所以有 (4) 设 (A) 【答案】(B) 【考点】定积分的基本性质 【难易度】★★ 解析:如图所示,因为 因此 (5) 设A为3阶矩阵,将A的第2列加到第1列得矩阵B,再交换B的第2行与第3行得单位矩阵,记 (A) 【答案】(D) 【考点】矩阵的初等变换 【难易度】★★ 【详解】 解析:由初等矩阵与初等变换的关系知 所以 (6) 设 (A) 【答案】(D) 【考点】★★★ 【难易度】矩阵的秩;齐次线性方程组的基础解系 【详解】 解析:由 (7) 设
![]()
![]()
![]()
![]()
![]()
![]()
![]() 时,原方程有三个根;当
时,原方程有三个根;当![]() 时,原方程有一个根.
时,原方程有一个根.![]()
![]() ;(II)
;(II) ![]() ,
,![]() ,
,![]()
![]() 的特征值为-1,1,0,对应的特征向量为
的特征值为-1,1,0,对应的特征向量为![]() ,
,![]() ,
,![]() (II)
(II) 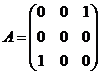
![]() 的概率分布为
的概率分布为
![]() 的概率分布为
的概率分布为

![]()
![]() ;(Ⅱ)
;(Ⅱ) ![]() ,
,![]()
![]() 的拐点是 ( )
的拐点是 ( )![]() (B)
(B) ![]() (C)
(C) ![]() (D)
(D) ![]()
![]() 可知
可知![]() 分别是
分别是![]() 的一、二、三、四重根,故由导数与原函数之间的关系可知
的一、二、三、四重根,故由导数与原函数之间的关系可知![]() ,
,![]()
![]() ,
,![]() ,
,![]() ,故(3,0)是一拐点.
,故(3,0)是一拐点.![]() 单调减少,
单调减少,![]() ,
,![]() 无界,则幂级数
无界,则幂级数![]() 的收敛域为 ( )
的收敛域为 ( )![]() (B)
(B) ![]() (C)
(C) ![]() (D)
(D) ![]()
![]() 无界,说明幂级数
无界,说明幂级数![]() 的收敛半径
的收敛半径![]() ;
;![]() 单调减少,
单调减少,![]() ,说明级数
,说明级数![]() 收敛,可知幂级数
收敛,可知幂级数![]() 的收敛半径
的收敛半径![]() .
.![]() 的收敛半径
的收敛半径![]() ,收敛区间为
,收敛区间为![]() .又由于
.又由于![]() 时幂级数收敛,
时幂级数收敛,![]() 时幂级数发散.可知收敛域为
时幂级数发散.可知收敛域为![]() .
.![]() 具有二阶连续导数,且
具有二阶连续导数,且![]() ,
,![]() ,则函数
,则函数![]() 在点
在点![]() 处取得极小值的一个充分条件是 ( )
处取得极小值的一个充分条件是 ( ) ![]() ,
,![]() (B)
(B) ![]() ,
,![]()
![]() ,
,![]() (D)
(D) ![]() ,
,![]()
![]() 知
知![]() ,
,![]()
![]() ,
,![]()
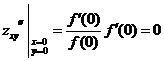 ,
,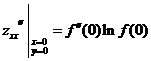 ,
,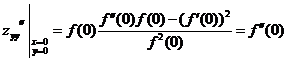
![]() 在点(0,0)处取得极小值,仅需
在点(0,0)处取得极小值,仅需![]() ,
,![]()
![]()
![]() ,
,![]() ,
,![]() ,则
,则![]() 的大小关系是( )
的大小关系是( ) ![]() (B)
(B) ![]() (C)
(C) ![]() (D)
(D) ![]()
 【详解】
【详解】![]() 时,
时,![]() ,
,![]()
![]() ,故选(B)
,故选(B)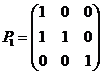 ,
,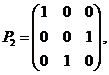 则A= ( )
则A= ( ) ![]() (B)
(B) ![]() (C)
(C) ![]() (D)
(D) ![]()
![]() ,
,![]() ,
,![]() ,故选(D)
,故选(D)![]() 是4阶矩阵,
是4阶矩阵,![]() 为
为![]() 的伴随矩阵,若
的伴随矩阵,若![]() 是方程组Ax=0的一个基础解系,则
是方程组Ax=0的一个基础解系,则![]() 的基础解系可为 ( )
的基础解系可为 ( ) ![]() (B)
(B) ![]() (C)
(C) ![]() (D)
(D) ![]()
![]() 的基础解系只有一个知
的基础解系只有一个知![]() ,所以
,所以![]() ,又由
,又由![]() 知,
知,![]() 都是
都是![]() 的解,且
的解,且![]() 的极大线生无关组就是其基础解系,又
的极大线生无关组就是其基础解系,又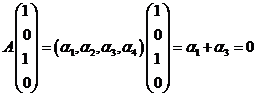 ,所以
,所以![]() 线性相关,故
线性相关,故![]() 或
或![]() 为极大无关组,故应选(D).
为极大无关组,故应选(D).![]() ,
,![]() 为两个分布函数,其相应的概率密度
为两个分布函数,其相应的概率密度![]() ,
,![]() 是连续函数,
是连续函数,