时间:2016-03-06 19:38:53
(A) ![]()
![]() (B)
(B) ![]()
![]()
![]()
(C) ![]()
![]() (D)
(D) ![]()
![]() +
+![]()
![]()
【答案】(D)
【考点】连续型随机变量的概率密度的性质
【难易度】★★
【详解】
解析:检验概率密度的性质:![]() ;
;
![]() .可知
.可知![]() 为概率密度,故选(
为概率密度,故选(![]() ).
).
(8) 设随机变量![]() 与
与![]() 相互独立,且
相互独立,且![]() 与
与![]() 存在,记
存在,记![]() 则
则![]() ( )
( )
(A) ![]() (B)
(B) ![]() (C)
(C) ![]() (D)
(D) ![]()
【答案】(B)
【考点】随机变量数学期望的性质
【难易度】★★
【详解】
解析:由于![]()
可知![]()
故应选(B)
二、填空题:9~14小题,每小题4分,共24分,请将答案写在答题纸指定位置上.
(9) 曲线![]() 的弧长
的弧长![]() .
.
【答案】 ![]()
【考点】定积分的几何应用—平面曲线的弧长
【难易度】★★★
【详解】
解析:![]()
![]() .
.
(10) 微分方程![]() 满足条件
满足条件![]() 的解为
的解为![]() .
.
【答案】 ![]()
【考点】一阶线性微分方程
【难易度】★★
【详解】
解析:原方程的通解为
![]()
由![]() ,得
,得![]() ,故所求解为
,故所求解为![]()
(11) 设函数![]() ,则
,则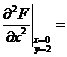 .
.
【答案】4
【考点】积分上限的函数及其导数;二阶偏导数
【难易度】★★
【详解】
解析:![]()
![]() ,故
,故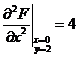 .
.
(12) 设![]() 是柱面
是柱面![]() 与平面
与平面![]() 的交线,从
的交线,从![]() 轴正向往
轴正向往![]() 轴负向看去为逆时针方向,则曲线积分
轴负向看去为逆时针方向,则曲线积分![]() .
.
【答案】 ![]()
【考点】第二类曲线积分的计算
【难易度】★★★★
【详解】
解析:曲线![]() 的参数方程为
的参数方程为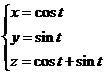 ,其中
,其中![]() 从
从![]() 到
到![]() .因此
.因此
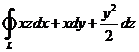
![]()
![]()
![]()
![]()
(13) 若二次曲面的方程![]() ,经正交变换化为
,经正交变换化为![]() ,则
,则![]() .
.
【答案】![]() .
.
【考点】二次型的标准形
【难易度】★★★
【详解】
解析:由于二次型通过正交变换所得到的标准形前面的系数为二次型对应矩阵![]() 的特征值,故
的特征值,故![]() 的特征值为0,1,4.由于二次型所对应的矩阵为
的特征值为0,1,4.由于二次型所对应的矩阵为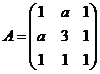
而![]() ,故
,故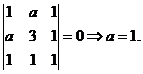
(14) 设二维随机变量![]() 服从正态分布
服从正态分布![]() ,则
,则![]() = .
= .
【答案】![]()
【考点】二维正态分布的性质
【难易度】★★
【详解】
解析:![]() ,由二维正态分布的性质可知随机变量
,由二维正态分布的性质可知随机变量![]() 独立.因此
独立.因此![]() .
.
由于![]() 服从
服从![]() ,可知
,可知![]() ,则
,则
![]() .
.
三、解答题:15~23小题,共94分.请将解答写在答题纸指定的位置上.解答应写出文字说明、证明过程或演算步骤.
(15) (本题满分10分)
求极限![]() .
.
【考点】两个重要极限;洛必达法则
【难易度】★★
【详解】
解析: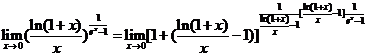
(![]() 时,
时,![]() ,
,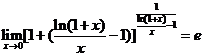 )
)
![]() (
(![]() 时,
时,![]() )
)
![]()
![]() .
.
(16) (本题满分9分)
设函数![]() ,其中函数
,其中函数![]() 具有二阶连续偏导数,函数
具有二阶连续偏导数,函数![]() 可导且在
可导且在![]() 处取得极值
处取得极值![]() ,求
,求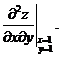
【考点】多元复合函数二阶偏导数的求法
【难易度】★★★
【详解】
解析:![]()
![]()
![]()
![]()
![]() 在
在![]() 可导,且为极值.
可导,且为极值.
![]() ,则
,则![]()
(17) (本题满分 10分)
求方程![]() 不同实根的个数,其中k为参数.
不同实根的个数,其中k为参数.
【考点】零点定理;函数单调性的判别
【难易度】★★★
【详解】
解析:令![]() ,则
,则![]() 是
是![]() 上的奇函数,且
上的奇函数,且
![]() ,
,![]() .
.
当![]() 即
即![]() 时,
时,![]() ,
,![]() 在
在![]() 内单调减少,方程
内单调减少,方程![]() 只有一个实根
只有一个实根![]() .
.
当![]() 即
即![]() 时,在
时,在![]() 内,
内,![]() ,
,![]() 单调增加;在
单调增加;在![]() 内,
内,![]() ,
,![]() 单调减少,所以
单调减少,所以![]() 是
是![]() 在
在![]() 内的最大值.
内的最大值.
由于![]() ,所以
,所以![]() .
.
又因为![]() ,所以存在
,所以存在![]() ,使得
,使得![]() .
.
由![]() 是奇函数及其单调性可知,当
是奇函数及其单调性可知,当![]() 时,方程
时,方程![]() 有且仅有三个不同实根
有且仅有三个不同实根![]() ,
,![]() ,
,![]() .
.
(18) (本题满分 10分)
(I)证明:对任意的正整数n,都有![]() 成立.
成立.
(II)设![]() ,证明数列
,证明数列![]() 收敛.
收敛.
【考点】单调有界准则;拉格朗日中值定理;比较审敛法
【难易度】★★★★
【详解】
证明:(I)设![]()
显然![]() 在
在![]() 上满足拉格朗日中值定理
上满足拉格朗日中值定理
![]()
![]() 时,
时,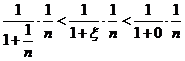 ,即
,即![]()
![]()
结论得证
(II)方法一:设![]() .
.
先证数列![]() 单调递减.
单调递减.
![]()
利用(I)的结论可以得到![]() ,所以
,所以![]() 得到
得到![]() ,即数列
,即数列![]() 单调递减.
单调递减.
再证数列![]() 有下界.
有下界.
![]()
![]()
![]()
得到数列![]() 有下界.
有下界.
利用单调递减数列且有下界得到![]() 收敛.
收敛.
方法二:设![]()
![]()
![]()
![]()
![]()
![]()
![]()
又![]()
![]()
![]()
又![]() 收敛
收敛
由正项级数的比较判别法可知:![]() 收敛
收敛
![]() 收敛
收敛
![]() 收敛
收敛
![]() 数列
数列![]() 收敛
收敛
(19) (本题满分11 分)
已知函数![]() 具有二阶连续偏导数,且
具有二阶连续偏导数,且![]() ,
,![]() ,
,![]() ,其中
,其中![]() ,计算二重积分
,计算二重积分![]() .
.
【考点】利用直角坐标计算二重积分;定积分的换元法;定积分的分部积分法
【难易度】★★★
【详解】
解析:![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
(20) (本题满分11 分)
设向量组![]() ,不能由向量组
,不能由向量组![]()
![]()
![]() 线性表示.
线性表示.
(I)求a的值;
(II)将![]() 用
用![]() 线性表示.
线性表示.
【考点】向量组线性相关的充分必要条件;向量的线性表示
【难易度】★★★
【详解】
解析:(I)因为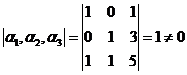 ,所以
,所以![]() 线性无关.
线性无关.
那么![]() 不能由
不能由![]() 线性表示
线性表示![]()
![]() 线性相关,即
线性相关,即
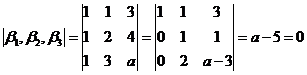 ,
,
所以![]()
(II)令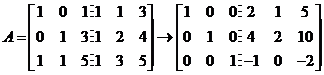
从而![]() ,
,![]() ,
,![]() .
.
(21) (本题满分11分)
设![]() 为3阶实对称矩阵,
为3阶实对称矩阵,![]() 的秩为2,且
的秩为2,且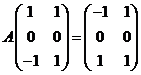 .
.
(I) 求![]() 的所有特征值与特征向量;
的所有特征值与特征向量;
(II)求矩阵![]() .
.
【考点】矩阵的特征值的概念、矩阵的特征向量的概念、实对称矩阵的特性、实对称矩阵的相似对角矩阵
【难易度】★★★
【详解】
解析:(I)因![]() 知
知![]() ,所以
,所以![]() 是
是![]() 的特征值.
的特征值.
又 ,
,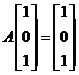 ,
,
所以-1,1是A的两个特征值,对应的特征向量分别为![]() ,
,![]() .
.
设![]() 是
是![]() 属于特征值0的特征向量.由于A为实对称矩阵,不同特征值对应的特征向量相互正交,因此
属于特征值0的特征向量.由于A为实对称矩阵,不同特征值对应的特征向量相互正交,因此
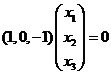 ,
,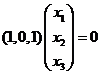 ,即
,即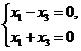
于是属于0的特征向量为![]() .
.
故矩阵A的特征值为-1,1,0;特征向量依次为![]() ,
,![]() ,
,![]() ,其中
,其中![]() 为任意非零常数.
为任意非零常数.
(II)令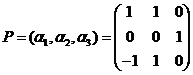 ,则
,则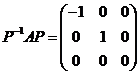 ,于是
,于是
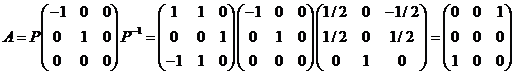
(22)(本题满分11分)
设随机变量![]() 与
与![]() 的概率分布分别为
的概率分布分别为
|
X |
|
|
|
P |
|
|
|
Y |
|
|
1 |
|
P |
|
|
|
且![]() .
.
(I) 求二维随机变量![]() 的概率分布;
的概率分布;
(II) 求![]() 的概率分布;
的概率分布;
(III) 求![]() 与
与![]() 的相关系数
的相关系数![]() .
.
【考点】二维离散型随机变量的概率分布;二维离散型随机变量分布函数的计算;相关系数的概念
【难易度】★★★
【详解】
解析:(I)由于![]() ,因此
,因此![]() .
.
故![]() .
.
![]()
![]() ,
,
![]() ,
,
![]() .
.
![]()
![]() 的概率分布为
的概率分布为

(II) ![]() 的所有可能取值为-1,0,1 .由
的所有可能取值为-1,0,1 .由![]() 的概率分布得
的概率分布得
![]() ,
,![]() ,
,
![]() .
.
![]() 的概率分布为
的概率分布为

(III)由X,Y及Z的概率分布得
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
![]()
![]() .
.
(23) (本题满分 11分)
设![]() 为来自正态总体
为来自正态总体![]() 的简单随机样本,其中
的简单随机样本,其中![]() 已知,
已知,![]() 未知.
未知.![]() 和
和![]() 分别表示样本均值和样本方差.
分别表示样本均值和样本方差.
(Ⅰ)求参数![]() 的最大似然估计
的最大似然估计![]() ;
;
(Ⅱ)计算![]() 和
和![]() .
.
【考点】最大似然估计法;![]() 分布;样本均值;样本方差
分布;样本均值;样本方差
【难易度】★★★★
【详解】
解析:![]() 的概率密度为
的概率密度为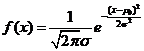 ,
,![]()
(Ⅰ)由题意可知 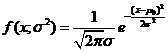
似然函数为 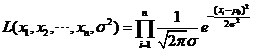
取对数,得 ![]()
![]()
令![]() ,可得
,可得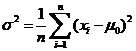 ,
,
则![]() 的最大似然估计量
的最大似然估计量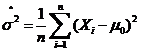 .
.
(Ⅱ)![]()
由于![]() ,由正态分布的性质可知
,由正态分布的性质可知![]() ,
,
![]()
由![]() 分布的方差可知
分布的方差可知![]() ,所以
,所以