时间:2016-03-06 19:02:50
2009年全国硕士研究生入学统一考试数学(一)试卷
一、选择题(1-8小题,每小题4分,共32分,下列每小题给出的四个选项中,只有一项符合题目要求,把所选项前的字母填在题后的括号内.)
(1)当
时,
与
等价无穷小,则
(A)
(B)
(C)
(D)
|
(2)如图,正方形 (A) (C)
|
|
(3)设函数
在区间
上的图形为
则函数
的图形为
(A) 
(B)
(C)
(D)
(4)设有两个数列
,若
,则
(A)当
收敛时,
收敛. (B)当发散时,发散.
(C)当
收敛时,
收敛. (D)当发散时,发散.
(5)设
是3维向量空间
的一组基,则由基
到基
的过渡矩阵为
(A)
(B)
(C)
(D)
(6)设
均为2阶矩阵,
分别为的伴随矩阵,若
,则分块矩阵
的伴随矩阵为
(A)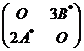
(B)
(C)
(D)
(7)设随机变量
的分布函数为
,其中
为标准正态分布函数,则
(A)0 (B)0.3
(C)0.7 (D)1
(8)设随机变量与
相互独立,且服从标准正态分布
,的概率分布为
,记
为随机变量
的分布函数,则函数的间断点个数为
(A)0 (B)1
(C)2 (D)3
二、填空题(9-14小题,每小题4分,共24分,请将答案写在答题纸指定位置上.)
(9)设函数
具有二阶连续偏导数,
,则
.
(10)若二阶常系数线性齐次微分方程
的通解为
,则非齐次方程
满足条件
的解为
.
(11)已知曲线
,则
.
(12)设
,则
.
(13)若3维列向量
满足
,其中
为
的转置,则矩阵
的非零特征值为 .
(14)设
为来自二项分布总体
的简单随机样本,
和
分别为样本均值和样本方差.若
为
的无偏估计量,则
.
三、解答题(15－23小题,共94分.请将解答写在答题纸指定的位置上.解答应写出文字说明、证明过程或演算步骤.)
(15)(本题满分9分)
求二元函数
的极值.
(16)(本题满分9分)
设
为曲线
与
所围成区域的面积,记
,求
与
的值.
(17)(本题满分11分)
椭球面是椭圆
绕
轴旋转而成,圆锥面是过点
且与椭圆相切的直线绕轴旋转而成.
(1)求及的方程. (2)求与之间的立体体积.
(18)(本题满分11分)
(1)证明拉格朗日中值定理:若函数
在
上连续,在
可导,则存在
,使得
.
(2)证明:若函数在
处连续,在
内可导,且
,则
存在,且
(19)(本题满分10分)
计算曲面积分
,其中
是曲面
的外侧.
(20)(本题满分11分)
设
,
(1)求满足
的
.
的所有向量,
. (2)对(1)中的任意向量,证明
无关.
(21)(本题满分11分)
设二次型
.
(1)求二次型
的矩阵的所有特征值; (2)若二次型的规范形为
,求
的值.
(22)(本题满分11分)
袋中有1个红色球,2个黑色球与3个白球,现有回放地从袋中取两次,每次取一球,以
分别表示两次取球所取得的红球、黑球与白球的个数.
(1) 求
. (2)求二维随机变量
概率分布
(23)(本题满分11 分)
设总体的概率密度为
,其中参数
未知,
,
,…
是来自总体的简单随机样本.
(1)求参数
的矩估计量.
(2)求参数的最大似然估计量.
2009年全国硕士研究生入学统一考试数学一试题及解析 一、选择题：1~8小题，每小题8分，共32分，下列每小题给出的四个选项中，只有一 符合题目要求，把所选项前的字母填在题后的括号内。 （1）当 （A） （C） 【分析】考查无穷小量比较的概念与极限运算法则或泰勒公式。 【详解】 法一：由题设 而对上极限式化简得： 要使极限存在，必须满足 又 故应选（A）。 法二：由于 因为 （2）如图，正方形 （A）
时，
与
等价无穷小，则
（B）
（D）
，从而
；
，所以
与
是等价无穷小量，所以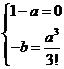
，从而，。故应选（A）。
被其对角线划分为四个区域，
，则
. （B）
. （C）
. （D）
