时间:2016-03-06 19:02:50
又由于![]() ,对上(*)式两边取
,对上(*)式两边取![]() 时的极限可得:
时的极限可得:
![]()
故![]() 存在,且
存在,且![]() 。
。
法二:利用洛必达法则:
![]()
由题设![]() ,故
,故![]() 存在,且
存在,且![]() 。
。
(19)(本题满分10分)
计算曲面积分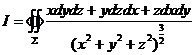 其中
其中![]() 是曲面
是曲面![]() 的外侧。
的外侧。
【分析】考查封闭曲面上第二类曲面积分的计算。首先在![]() 所围立体内做有向闭曲面
所围立体内做有向闭曲面![]() 挖去“瑕点” ,然后分别利用高斯公式计算。
挖去“瑕点” ,然后分别利用高斯公式计算。
【详解】![]() ,其中
,其中![]()
因为 ![]() ①
①
![]() ②
②
![]() ③
③
所以①+②+③=![]()
由于被积函数及其偏导数在点(0,0,0)处不连续,不能直接使用高斯公式。
令 ![]() (其中
(其中![]() 为很小的正数,使得
为很小的正数,使得![]() 在
在![]() 所围立体内),取内侧。有
所围立体内),取内侧。有
![]()
![]()
![]()
![]()
评注:在计算线积分或面积分时,可以将积分曲面或积分曲线的方程带入被积函数化简。
(20)(本题满分11分)
设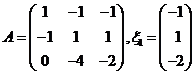
(I)求满足![]() 的所有向量
的所有向量![]() ;
;
(II)对(I)中的任一向量![]() ,证明:
,证明:![]() 线性无关。
线性无关。
【分析】本题考查矩阵的运算、非齐次线性方程组求解、解的结构,线性无关的判定(三个三维向量线性无关的充要条件是行列式不为零),行列式的计算等。
【详解】(I)解方程![]() ,
,
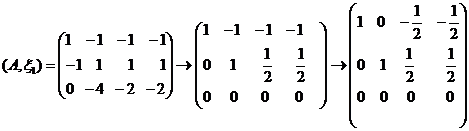 。
。
故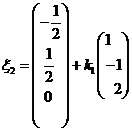 ,其中
,其中![]() 为任意常数。
为任意常数。
解方程组![]() ,由于
,由于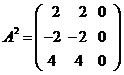 ,而
,而
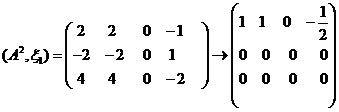
故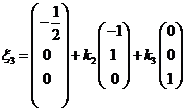 ,其中
,其中![]() 为任意常数。
为任意常数。
(II)法一:由于
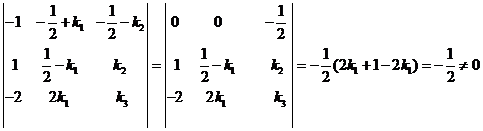 。
。
故![]() 线性无关。
线性无关。
法二:由题设可知:![]() 。设存在常数
。设存在常数![]() ,使得
,使得
![]() -------------------------------①
-------------------------------①
用![]() 左乘①式两端得:
左乘①式两端得:![]() ,所以
,所以![]() ,即
,即![]() ------------------------------②
------------------------------②
用![]() 左乘②式两端得:
左乘②式两端得:![]() ,所以
,所以![]() ,即
,即![]() ,所以
,所以![]() ,代入②得
,代入②得![]() ,最后由①得
,最后由①得![]() 。从而
。从而![]() 线性无关。
线性无关。
(21)(本题满分11分)
设二次型![]()
(Ⅰ)求二次型![]() 的矩阵的所有特征值;
的矩阵的所有特征值;
(Ⅱ)若二次型![]() 的规范形为
的规范形为![]() ,求
,求![]() 的值。
的值。
【分析】本题考查二次型的矩阵、求矩阵的特征值、二次型的规范形、惯性定理等。题中二次型带有参数![]() ,所以其特征值也会含有
,所以其特征值也会含有![]() ,在计算其特征多项式时要仔细。第(Ⅱ)问的关键是对规范形的理解。二次型的规范形所提供的信息是其秩及正惯性指数分别是多少,正是由此知道该二次型有两个特征值为正,一个为零,从而可以确定
,在计算其特征多项式时要仔细。第(Ⅱ)问的关键是对规范形的理解。二次型的规范形所提供的信息是其秩及正惯性指数分别是多少,正是由此知道该二次型有两个特征值为正,一个为零,从而可以确定![]() 的值。
的值。
【详解】(I)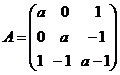 。
。
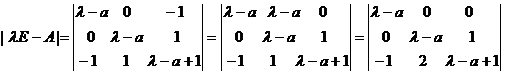
![]() 。
。
所以二次型的矩阵A的特征值为![]() 、
、![]() 、
、![]() 。
。
(II)法一:若二次型![]() 的规范形为
的规范形为![]() ,说明有两个特征值为正,一个为0。则
,说明有两个特征值为正,一个为0。则
若![]() ,则
,则 ![]() ,
,![]() ,不符题意;
,不符题意;
若![]() ,即
,即![]() ,则
,则![]() ,
,![]() ,符合题意;
,符合题意;
若![]() ,即
,即![]() ,则
,则![]() ,
,![]() ,不符题意。
,不符题意。
综上所述,故![]()
法二:由![]() 的规范形为
的规范形为![]() 知,其矩阵
知,其矩阵![]() 的特征值有两个为正数,一个为零。又
的特征值有两个为正数,一个为零。又![]() ,所以
,所以![]() ,即
,即![]() 。
。
(22)(本题满分 11 分)
袋中有1个红色球,2个黑色球与3个白球,现有放回地从袋中取两次,每次取一球,以![]() 分别表示两次取球所取得的红球、黑球与白球的个数。
分别表示两次取球所取得的红球、黑球与白球的个数。
(Ⅰ)求![]() ;
;
(Ⅱ)求二维随机变量![]() 的概率分布。
的概率分布。
【分析】本题属于古典概型的题目,只要用排列组合的技巧就可以解决。(Ⅰ)的计算也可利用条件概率公式,关键是计算![]() 和
和![]() 。
。
【详解】(I)法一:在没有取白球的情况下取了一次红球,利用样本空间的缩减法,相当于只有 1个红球,2 个黑球放回摸两次,其中摸一个红球的概率,所以
![]() 。
。
法二: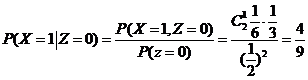 ;
;
(II)![]() 取值范围为0,1,2,故
取值范围为0,1,2,故
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,![]()
|
Y X |
0 |
1 |
2 |
|
0 |
1/4 |
1/6 |
1/36 |
|
1 |
1/3 |
1/9 |
0 |
|
2 |
1/9 |
0 |
0 |
(23)(本题满分 11 分)
设总体![]() 的概率密度为
的概率密度为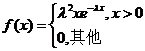 ,其中参数
,其中参数![]() 未知,
未知,![]() ,
,![]() ,…
,…![]() 是来自总体
是来自总体![]() 的简单随机样本
的简单随机样本
(Ⅰ)求参数![]() 的矩估计量;
的矩估计量;
(Ⅱ)求参数![]() 的最大似然估计量
的最大似然估计量
【分析】 本题考查矩估计和最大似然估计,利用固定的解法步骤完成即可。
【详解】(I)由![]() ,令
,令![]() ,可得总体参数
,可得总体参数![]() 的矩估计量
的矩估计量![]() 。
。
(II)构造似然函数
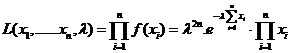
取对数![]()
令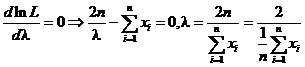 ,故其最大似然估计量为
,故其最大似然估计量为![]() 。
。