时间:2016-03-06 13:22:11
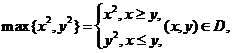
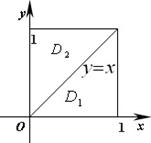 于是要用分块积分法,用
于是要用分块积分法,用![]() 将
将![]() 分成两块:
分成两块:
![]()
![]()
![]()
![]()
![]() (
(![]() 关于
关于![]() 对称)
对称)
![]() (选择积分顺序)
(选择积分顺序)![]()
六、【分析与求解】 (1)易知![]() 原函数,
原函数,
![]()
![]()
![]() 在
在![]() 上
上![]() 原函数,即
原函数,即![]() .
.
![]() 积分
积分![]() 在
在![]() 与路径无关.
与路径无关.
(2)因找到了原函数,立即可得![]()
七、【证明】 与书上解答略有不同,参见数三2002第七题(1)因为幂级数
![]()
的收敛域是![]() ,因而可在
,因而可在![]() 上逐项求导数,得
上逐项求导数,得
![]() ,
,
![]() ,
,
所以 ![]()
![]() .
.
(2)与![]() 相应的齐次微分方程为
相应的齐次微分方程为![]() ,
,
其特征方程为![]() ,特征根为
,特征根为![]() .
.
因此齐次微分方程的通解为![]() .
.
设非齐次微分方程的特解为![]() ,将
,将![]() 代入方程
代入方程![]() 可得
可得
![]() ,即有
,即有![]() .
.
于是,方程通解为![]() .
.
当![]() 时,有
时,有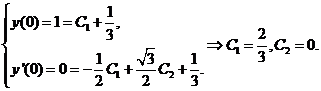
于是幂级数![]() 的和函数为
的和函数为![]()
![]()
八、【分析与求解】 (1)由梯度向量的重要性质:函数![]() 在点
在点![]() 处沿该点的梯度方向
处沿该点的梯度方向
![]()
方向导数取最大值即![]() 的模,
的模,![]()
(2)按题意,即求![]() 求在条件
求在条件![]() 下的最大值点
下的最大值点![]()
![]()
在条件![]() 下的最大值点.
下的最大值点.
这是求解条件最值问题,用拉格朗日乘子法.令拉格朗日函数
![]()
则有 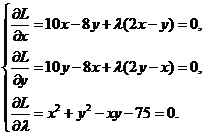
解此方程组:将①式与②式相加得![]() 或
或![]()
若![]() ,则由③式得
,则由③式得![]() 即
即![]() 若
若![]() 由①或②均得
由①或②均得![]() ,代入③式得
,代入③式得![]() 即
即![]() 于是得可能的条件极值点
于是得可能的条件极值点
![]()
现比较![]() 在这些点的函数值:
在这些点的函数值:
![]()
因为实际问题存在最大值,而最大值又只可能在![]() 中取到.因此
中取到.因此![]() 在
在![]() 取到在
取到在![]() 的边界上的最大值,即
的边界上的最大值,即![]() 可作为攀登的起点.
可作为攀登的起点.
九、【解】 由![]() 线性无关及
线性无关及![]() 知,向量组的秩
知,向量组的秩![]() ,即矩阵
,即矩阵![]() 的秩为
的秩为![]() 因此
因此![]() 的基础解系中只包含一个向量.那么由
的基础解系中只包含一个向量.那么由
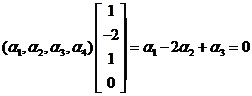
知,![]() 的基础解系是
的基础解系是![]()
再由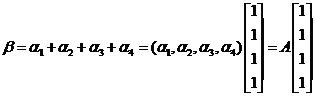 知,
知,![]() 是
是![]() 的一个特解.故
的一个特解.故![]() 的通解是
的通解是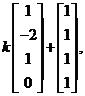 其中
其中![]() 为任意常数.
为任意常数.
十、【解】 (1)若![]() 相似,那么存在可逆矩阵
相似,那么存在可逆矩阵![]() ,使
,使![]() 故
故
![]()
![]()
(2)令![]() 那么
那么![]()
但![]() 不相似.否则,存在可逆矩阵
不相似.否则,存在可逆矩阵![]() ,使
,使![]() .从而
.从而![]() ,矛盾,亦可从
,矛盾,亦可从![]() 而知
而知![]() 与
与![]() 不相似.
不相似.
(3)由![]() 均为实对称矩阵知,
均为实对称矩阵知,![]() 均相似于对角阵,若
均相似于对角阵,若![]() 的特征多项式相等,记特征多项式的根为
的特征多项式相等,记特征多项式的根为![]() 则有
则有
![]() 相似于
相似于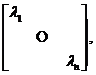
![]() 也相似于
也相似于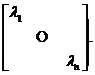
即存在可逆矩阵![]() ,使
,使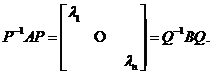
于是![]() 由
由![]() 为可逆矩阵知,
为可逆矩阵知,![]() 与
与![]() 相似.
相似.
十一、【解】 由于![]() 依题意,
依题意,![]() 服从二项分布
服从二项分布![]() ,则有
,则有
![]()
十二、【解】 ![]()
![]()
![]() 的矩估计量为
的矩估计量为![]() 根据给定的样本观察值计算
根据给定的样本观察值计算![]()
![]() 因此
因此![]() 的矩估计值
的矩估计值![]()
对于给定的样本值似然函数为
![]()
![]()
令![]() ,得方程
,得方程![]() ,解得
,解得![]() (
(![]() 不合题意).
不合题意).
于是![]() 的最大似然估计值为
的最大似然估计值为![]()