时间:2016-03-06 12:47:36
一、填空题(本题共5个小题,每小题3分,满分15分.)
(1) ![]() ______________.
______________.
(2) ![]() ______________.
______________.
(3) 设![]() ,则
,则![]() ______________.
______________.
(4) 幂级数![]() 的收敛半径
的收敛半径![]() ______________.
______________.
(5) 设三阶方阵![]() 、
、![]() 满足关系式:
满足关系式:![]() ,且
,且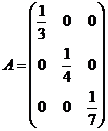 ,则
,则![]()
______________.
二、选择题(本题共5个小题,每小题3分,满分15分.)
(1) 设有直线![]() 及平面
及平面![]() ,则直线
,则直线![]() ( )
( )
(A) 平行于![]() (B) 在
(B) 在![]() 上 (C) 垂直于
上 (C) 垂直于![]() (D) 与
(D) 与![]() 斜交
斜交
(2) 设在![]() 上
上![]() ,则
,则![]() 、
、![]() 、
、![]() 或
或![]() 的大小顺序是
的大小顺序是
( )
(A) ![]() (B)
(B) ![]()
(C) ![]() (D)
(D) ![]()
(3) 设![]() 可导,
可导,![]() ,则
,则![]() 是
是![]() 在
在![]() 处可导的 ( )
处可导的 ( )
(A) 充分必要条件 (B) 充分条件但非必要条件
(C) 必要条件但非充分条件 (D) 既非充分条件又非必要条件
(4) 设![]() ,则级数 ( )
,则级数 ( )
(A) ![]() 与
与![]() 都收敛 (B)
都收敛 (B) ![]() 与
与![]() 都发散
都发散
(C) ![]() 收敛而
收敛而![]() 发散 (D)
发散 (D) ![]() 发散而
发散而![]() 收敛
收敛
(5) 设 ,
, ,
,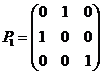 ,
,
 ,则必有 ( )
,则必有 ( )
(A) ![]() (B)
(B) ![]()
(C) ![]() (D)
(D) ![]()
三、(本题共2小题,每小题5分,满分10分.)
(1) 设![]() ,其中
,其中![]() 、
、![]() 都具有一阶连续偏导数,且
都具有一阶连续偏导数,且
![]() ,求
,求![]() .
.
(2) 设函数![]() 在区间
在区间![]() 上连续,并设
上连续,并设![]() ,求
,求 ![]() .
.
四、(本题共2小题,每小题6分,满分12分.)
(1) 计算曲面积分![]() ,其中
,其中![]() 为锥面
为锥面![]() 在柱体
在柱体![]() 内的部分.
内的部分.
(2) 将函数![]() 展开成周期为4的余弦级数.
展开成周期为4的余弦级数.
五、(本题满分7分)
设曲线![]() 位于
位于![]() 平面的第一象限内,
平面的第一象限内,![]() 上任一点
上任一点![]() 处的切线与
处的切线与![]() 轴总相交,交点记为
轴总相交,交点记为![]() .已知
.已知![]() ,且
,且![]() 过点
过点![]() ,求
,求![]() 的方程.
的方程.
六、(本题满分8分)
设函数![]() 在
在![]() 平面上具有一阶连续偏导数,曲线积分
平面上具有一阶连续偏导数,曲线积分![]() 与路径无关,并且对任意
与路径无关,并且对任意![]() 恒有
恒有
![]() ,
,
求![]() .
.
七、(本题满分8分)
假设函数![]() 和
和![]() 在
在![]() 上存在二阶倒数,并且
上存在二阶倒数,并且
![]() ,
,![]() ,试证:
,试证:
(1) 在开区间![]() 内
内![]() ;
;
(2) 在开区间![]() 内至少存在一点
内至少存在一点![]() ,使
,使![]() .
.
八、(本题满分7分)
设三阶实对称矩阵![]() 的特征值为
的特征值为![]() ,
,![]() ,对应于
,对应于![]() 的特征向量为
的特征向量为
![]() ,求
,求![]() .
.
九、(本题满分6分)
设![]() 是
是![]() 阶矩阵,满足
阶矩阵,满足![]() (
(![]() 是
是![]() 阶单位阵,
阶单位阵,![]() 是
是![]() 的转置矩阵),
的转置矩阵),![]() ,求
,求
![]() .
.
十、填空题(本题共2小题,每小题3分,满分6分.)
(1) 设![]() 表示10次独立重复射击命中目标的次数,每次射中目标的概率为0.4,则
表示10次独立重复射击命中目标的次数,每次射中目标的概率为0.4,则![]() 的数学期望
的数学期望![]() ___________.
___________.
(2) 设![]() 和
和![]() 为两个随机变量,且
为两个随机变量,且
![]() ,
, ![]() ,
,
则![]() ___________.
___________.
十一、(本题满分6分)
设随机变量![]() 的概率密度为
的概率密度为 求随机变量
求随机变量![]() 的概率密度
的概率密度
![]() .
.
一、填空题(本题共5个小题,每小题3分,满分15分.)
(1)【答案】![]()
【解析】这是![]() 型未定式求极限,
型未定式求极限,
![]() ,
,
令![]() ,则当
,则当![]() 时,
时,![]() ,所以
,所以
![]() ,
,
故 ![]() .
.
(2)【答案】![]()
【解析】 ![]()
![]()
![]() .
.
【相关知识点】积分上限函数的求导公式:
![]() .
.
(3)【答案】![]()
【解析】利用向量运算律有
![]()
![]()
![]() (其中
(其中![]() )
)
![]()
![]()
![]() .
.
(4)【答案】![]()
【解析】令![]() ,则当
,则当![]() 时,有
时,有
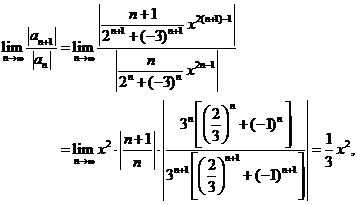
而当![]() 时,幂级数收敛,即
时,幂级数收敛,即![]() 时,此幂级数收敛,当
时,此幂级数收敛,当![]() 时,即
时,即![]() 时,此幂级数发散,因此收敛半径为
时,此幂级数发散,因此收敛半径为![]() .
.
(5)【答案】
【解析】在已知等式![]() 两边右乘以
两边右乘以![]() ,得
,得![]() ,即
,即
![]() .
.
因为  ,所以
,所以
![]()
 =
= .
.
二、选择题(本题共5个小题,每小题3分,满分15分.)
(1)【答案】(C)
【解析】这是讨论直线![]() 的方向向量与平面
的方向向量与平面![]() 的法向量的相互关系问题.
的法向量的相互关系问题.
直线![]() 的方向向量
的方向向量
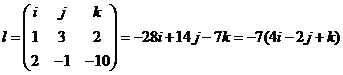 ,
,
平面![]() 的法向量
的法向量![]() ,
,![]() ,
,![]() .应选(C).
.应选(C).
(2)【答案】(B)
【解析】由![]() 可知
可知![]() 在区间
在区间![]() 上为严格单调递增函数,故
上为严格单调递增函数,故
![]()
由微分中值定理,![]() .所以
.所以
![]() ,
,![]()
故应选择(B).
(3)【答案】(A)
【解析】由于利用观察法和排除法都很难对本题作出选择,必须分别验证充分条件和必要条件.
充分性:因为![]() ,所以
,所以
![]() ,
,
由此可得 ![]() 在
在![]() 处可导.
处可导.
必要性:设![]() 在
在![]() 处可导,则
处可导,则![]() 在
在![]() 处可导,由可导的充要条件知
处可导,由可导的充要条件知
![]() . ①
. ①
根据重要极限![]() ,可得
,可得
![]() ,
,![]() , ②
, ②
结合①,②,我们有![]() ,故
,故![]() .应选(A).
.应选(A).
(4)【答案】(C)
【解析】这是讨论![]() 与
与![]() 敛散性的问题.
敛散性的问题.
![]() 是交错级数,显然
是交错级数,显然![]() 单调下降趋于零,由莱布尼兹判别法知,该级数收敛.
单调下降趋于零,由莱布尼兹判别法知,该级数收敛.
正项级数![]() 中,
中,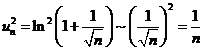 .
.
根据正项级数的比较判别法以及![]() 发散,
发散,![]() 发散.因此,应选(C).
发散.因此,应选(C).
【相关知识点】正项级数的比较判别法:
设![]() 和
和![]() 都是正项级数,且
都是正项级数,且![]() 则
则
⑴ 当![]() 时,
时,![]() 和
和![]() 同时收敛或同时发散;
同时收敛或同时发散;
⑵ 当![]() 时,若
时,若![]() 收敛,则
收敛,则![]() 收敛;若
收敛;若![]() 发散,则
发散,则![]() 发散;
发散;
⑶ 当![]() 时,若
时,若![]() 收敛,则
收敛,则![]() 收敛;若
收敛;若![]() 发散,则
发散,则![]() 发散.
发散.
(5)【答案】(C)
【解析】![]() 是交换单位矩阵的第一、二行所得初等矩阵,
是交换单位矩阵的第一、二行所得初等矩阵,![]() 是将单位矩阵的第一行加到第三行所得初等矩阵;
是将单位矩阵的第一行加到第三行所得初等矩阵;
而![]() 是由
是由![]() 先将第一行加到第三行,然后再交换第一、二行两次初等交换得到的,因此
先将第一行加到第三行,然后再交换第一、二行两次初等交换得到的,因此 ![]() ,故应选(C).
,故应选(C).
三、(本题共2小题,每小题5分,满分10分.)
(1)【解析】这实质上已经变成了由方程式确定的隐函数的求导与带抽象函数记号的复合函数求导相结合的问题.
先由方程式![]() ,其中
,其中![]() 确定
确定![]() ,并求
,并求![]() .
.
将方程两边对![]() 求导得
求导得
![]() ,
,
解得 ![]() . ①
. ①
现再将![]() 对
对![]() 求导,其中
求导,其中![]() ,
,![]() ,
,
可得 ![]() .
.
将①式代入得 &nbs