时间:2016-03-06 12:25:41
一、填空题(本题共5个小题,每小题3分,满分15分.)
(1) 
_____________.
(2) 曲面
在点(1,2,0)处的切平面方程为_____________.
(3) 设
,则
在点
处的值为_____________.
(4) 设区域
为
,则
_____________.
(5) 已知
,设
,其中
是
的转置,则
_________.
二、选择题(本题共5个小题,每小题3分,满分15分.)
(1) 设
,
,
,
则 ( )
(A) 
(B) 
(C) 
(D) 
(2) 二元函数
在点
处两个偏导数
、
存在是在该点连续的 ( )
(A) 充分条件但非必要条件 (B) 必要条件而非充分条件
(C) 充分必要条件 (D) 既非充分条件又非必要条件
(3) 设常数
,且级数
收敛,则级数
( )
(A) 发散 (B) 条件收敛
(C) 绝对收敛 (D) 收敛性与
有关
(4) 
,其中
,则必有 ( )
(A) 
(B) 
(C) 
(D) 
(5) 已知向量组
线性无关,则向量组 ( )
(A) 
、
、
、
线性无关
(B) 
、
、
、
线性无关
(C) 、、、线性无关
(D) 、、、线性无关
三、(本题共3小题, 每小题5分,满分15分.)
(1) 设
求
、
在
的值.
(2) 将函数
展开成
的幂级数.
(3) 求
.
四、(本题满分6分)
计算曲面积分
,其中
是由曲面
及两平面
所围成立体表面的外侧.
五、(本题满分9分)
设
具有二阶连续导数,
,且
为一全微分方程,求及此全微分方程的通解.
六、(本题满分8分)
设在点
的某一领域内具有二阶连续导数,且
,证明级数
绝对收敛.
七、(本题满分6分)
已知点
与
的直角坐标分别为(1,0,0)与(0,1,1).线段
绕
轴旋转一周所围成的旋转曲面为.求由及两平面
所围成的立体体积.
八、(本题满分8分)
设四元线性齐次方程组
为
又已知某线性齐次方程组
的通解为
.
(1) 求线性方程组的基础解系；
(2) 问线性方程组和是否有非零公共解？若有,则求出所有的非零公共解.若没有,则说明理由.
九、(本题满分6分)
设为
阶非零方阵,
是的伴随矩阵,
是的转置矩阵,当
时,证明
.
十、填空题(本题共2小题, 每小题3分,满分6分.)
(1) 已知、两个事件满足条件
,且
,则
__________.
(2) 设相互独立的两个随机变量
、
具有同一分布律,且的分布律为
|
|
|
|
|
|
则随机变量
的分布律为_______.
十一、(本题满分6分)
已知随机变量
服从二维正态分布,且和分别服从正态分布
和
,与的相关系数
,设
,
(1) 求
的数学期望
和方差
；
(2) 求与的相关系数
；
(3) 问与是否相互独立？为什么？
一、填空题(本题共5个小题,每小题3分,满分15分.)
(1)【答案】
【解析】原式变形后为“
”型的极限未定式,又分子分母在点
处导数都存在,所以连续应用两次洛必达法则,有
原式
. (由重要极限
)
(2)【答案】
【解析】所求平面的法向量为平行于所给曲面在点
处法线方向的方向向量
,取
,又平面过已知点
.
已知平面的法向量
和过已知点
可唯一确定这个平面：
.
因点在曲面
上.曲面方程
.
曲面在该点的法向量
,
故切平面方程为 
, 即 .
(3)【答案】
【解析】由于混合偏导数在连续条件下与求导次序无关,为了简化运算,所以本题可以先求
,再求
.
,
.
(可边代值边计算,这样可以简化运算量.)
【相关知识点】多元复合函数求导法则：如果函数
都在点
具有对及对
的偏导数,函数
在对应点
具有连续偏导数,则复合函数
在点的两个偏导数存在,且有
；
.
(4)【答案】
【解析】很显然,根据此题的特征用极坐标变换来计算：
原式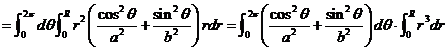
.
注意： 
,
则 原式
.
(5)【答案】
【解析】由矩阵乘法有结合律,注意 
是一个数,
而 
,(是一个三阶矩阵)
于是,
.
二、选择题(本题共5个小题,每小题3分,满分15分.)
(1)【答案】(D)
【解析】对于关于原点对称的区间上的积分,应该关注被积函数的奇偶性.
由对称区间上奇偶函数积分的性质,被积函数是奇函数,积分区间关于原点对称,则积分为0,故
,且
由定积分的性质,如果在区间
上,被积函数
,则
.
所以 &nb
