时间:2016-03-06 11:29:20
一、填空题(本题满分15分,每小题3分.)
(1) 设 则
则![]() =__________.
=__________.
(2) 由方程![]() 所确定的函数
所确定的函数![]() 在点
在点![]() 处的全微分
处的全微分![]() =__________.
=__________.
(3) 已知两条直线的方程是![]() ;
;![]() ,则过
,则过![]() 且平行于
且平行于![]() 的平面方程是__________.
的平面方程是__________.
(4) 已知当![]() 时,
时,![]() 与
与![]() 是等价无穷小,则常数
是等价无穷小,则常数![]() =__________.
=__________.
(5) 设4阶方阵 ,则
,则![]() 的逆阵
的逆阵![]() =__________.
=__________.
二、选择题(本题满分15分,每小题3分.)
(1) 曲线![]() ( )
( )
(A) 没有渐近线 (B) 仅有水平渐近线
(C) 仅有铅直渐近线 (D) 既有水平渐近线又有铅直渐近线
(2) 若连续函数![]() 满足关系式
满足关系式![]() ,则
,则![]() 等于 ( )
等于 ( )
(A) ![]() (B)
(B) ![]()
(C) ![]() (D)
(D) ![]()
(3) 已知级数![]() ,
,![]() ,则级数
,则级数![]() 等于 ( )
等于 ( )
(A) 3 (B) 7 (C) 8 (D) 9
(4) 设![]() 是
是![]() 平面上以(1,1)、(-1,1)和(-1,-1)为顶点的三角形区域,
平面上以(1,1)、(-1,1)和(-1,-1)为顶点的三角形区域,![]() 是
是![]() 在第一象限的部分,则
在第一象限的部分,则![]() 等于 ( )
等于 ( )
(A) ![]() (B)
(B) ![]()
(C) ![]() (D) 0
(D) 0
(5) 设![]() 阶方阵
阶方阵![]() 、
、![]() 、
、![]() 满足关系式
满足关系式![]() ,其中
,其中![]() 是
是![]() 阶单位阵,则必有 ( )
阶单位阵,则必有 ( )
(A) ![]() (B)
(B) ![]()
(C) ![]() (D)
(D) ![]()
三、(本题满分15分,每小题5分.)
(1) 求![]() .
.
(2) 设![]() 是曲面
是曲面![]() 在点
在点![]() 处的指向外侧的法向量,求函数
处的指向外侧的法向量,求函数
![]() 在点
在点![]() 处沿方向
处沿方向![]() 的方向导数.
的方向导数.
(3) ![]() ,其中
,其中![]() 是由曲线
是由曲线 绕
绕![]() 轴旋转一周而成的曲面与平面
轴旋转一周而成的曲面与平面![]() 所围成的立体.
所围成的立体.
四、(本题满分6分)
在过点![]() 和
和![]() 的曲线族
的曲线族![]() 中,求一条曲线
中,求一条曲线![]() ,使沿该曲线从
,使沿该曲线从![]() 到
到![]() 的积分
的积分![]() 的值最小.
的值最小.
五、(本题满分8分.)
将函数![]() 展开成以2为周期的傅立叶级数,并由此求级数
展开成以2为周期的傅立叶级数,并由此求级数
![]() 的和.
的和.
六、(本题满分7分.)
设函数![]() 在[0,1]上连续,(0,1)内可导,且
在[0,1]上连续,(0,1)内可导,且![]() ,证明在(0,1)内存在一点
,证明在(0,1)内存在一点![]() ,使
,使![]() .
.
七、(本题满分8分.)
已知![]() ,
,![]() ,
,![]() ,
,![]() ,及
,及
![]() .
.
(1) ![]() 、
、![]() 为何值时,
为何值时,![]() 不能表示成
不能表示成![]() 的线性组合?
的线性组合?
(2) ![]() 、
、![]() 为何值时,
为何值时,![]() 有
有![]() 的唯一的线性表示式?并写出该表示式.
的唯一的线性表示式?并写出该表示式.
八、(本题满分6分)
设![]() 为
为![]() 阶正定阵,
阶正定阵,![]() 是
是![]() 阶单位阵,证明
阶单位阵,证明![]() 的行列式大于1.
的行列式大于1.
九、(本题满分8分)
在上半平面求一条向上凹的曲线,其上任一点![]() 处的曲率等于此曲线在该点的法线段
处的曲率等于此曲线在该点的法线段![]() 长度的倒数(
长度的倒数(![]() 是法线与
是法线与![]() 轴的交点),且曲线在点(1,1)处的切线与
轴的交点),且曲线在点(1,1)处的切线与![]() 轴平行.
轴平行.
十、填空题(本题满分6分,每小题3分.)
(1) 若随机变量![]() 服从均值为2,方差为
服从均值为2,方差为![]() 的正态分布,且
的正态分布,且![]() ,则
,则
![]() =_______.
=_______.
(2) 随机地向半圆![]() (
(![]() 为正常数)内掷一点,点落在半圆内任何区域的概率与区域的面积成正比,则原点和该点的连线与
为正常数)内掷一点,点落在半圆内任何区域的概率与区域的面积成正比,则原点和该点的连线与![]() 轴的夹角小于
轴的夹角小于![]() 的概率为_______.
的概率为_______.
十一、(本题满分6分)
设二维随机变量![]() 的概率密度为
的概率密度为
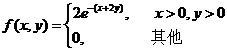 ,
,
求随机变量![]() 的分布函数.
的分布函数.
一、填空题(本题满分15分,每小题3分.)
(1)【答案】![]()
【解析】这是个函数的参数方程,满足参数方程所确定函数的微分法,即
如果 ![]() , 则
, 则 ![]() .
.
所以  ,
,
再对![]() 求导,由复合函数求导法则得
求导,由复合函数求导法则得
![]()
![]() .
.
(2)【答案】![]()
【解析】这是求隐函数在某点的全微分,这里点![]() 的含义是
的含义是![]() .
.
将方程两边求全微分,由一阶全微分形式不变性得
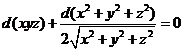 ,
,
再由全微分四则运算法则得
![]() ,
,
令![]() ,得
,得![]() ,即
,即![]() .
.
(3)【答案】![]()
【解析】所求平面![]() 过直线
过直线![]() ,因而过
,因而过![]() 上的点
上的点![]() ;
;
因为![]() 过
过![]() 平行于
平行于![]() ,于是
,于是![]() 平行于
平行于![]() 和
和![]() 的方向向量,即
的方向向量,即![]() 平行于向量
平行于向量![]() 和向量
和向量![]() ,且两向量不共线,于是平面
,且两向量不共线,于是平面![]() 的方程
的方程
 ,
,
即![]() .
.
(4)【答案】![]()
【解析】因为当![]() 时,
时,![]() ,
,
当![]() 时
时![]() ,所以有
,所以有
![]()
所以  .
.
因为当![]() 时,
时,![]() 与
与![]() 是等价无穷小,所以
是等价无穷小,所以![]() ,故
,故![]() .
.
(5)【答案】 .
.
【解析】为求矩阵的逆可有多种办法,可用伴随,可用初等行变换,也可用分块求逆.根据本题的特点,若知道分块求逆法,则可以简单解答.
注意: 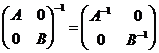 ,
, .
.
对于2阶矩阵的伴随矩阵有规律:![]() ,则求
,则求![]() 的伴随矩阵
的伴随矩阵
 .
.
如果![]() ,这样
,这样
 .
.
再利用分块矩阵求逆的法则: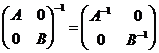 ,易见
,易见
 .
.
二、选择题(本题共5个小题,每小题3分,满分15分.)
(1)【答案】(D)
【解析】由于函数的定义域为![]() ,所以函数的间断点为
,所以函数的间断点为![]() ,
,
![]() ,所以
,所以![]() 为铅直渐近线,
为铅直渐近线,
![]() ,所以
,所以![]() 为水平渐近线.
为水平渐近线.
所以选(D).
【相关知识点】铅直渐近线:如函数![]() 在其间断点
在其间断点![]() 处有
处有![]() ,则
,则![]() 是函数的一条铅直渐近线;
是函数的一条铅直渐近线;
水平渐近线:当![]() ,则
,则![]() 为函数的水平渐近线.
为函数的水平渐近线.
(2)【答案】(B)
【解析】令![]() ,则
,则![]() ,所以
,所以
![]() ,
,
两边对![]() 求导,得
求导,得![]() ,这是一个变量可分离的微分方程,即
,这是一个变量可分离的微分方程,即![]() .解之得
.解之得![]() ,其中
,其中![]() 是常数.
是常数.
又因为![]() ,代入
,代入![]() ,得
,得![]() ,得
,得
![]() ,即
,即![]() .
.
(3)【答案】(C)
【解析】因为
![]()
![]()
![]() (收敛级数的结合律与线性性质),
(收敛级数的结合律与线性性质),
所以 ![]() .
.
而 ![]()
![]()
![]() ,
,
故应选(C).
(4) 【答案】(A)
【答案】(A)
【解析】如图,将区域![]() 分为
分为![]() 四个子区域.
四个子区域.
显然,![]() 关于
关于![]() 轴对称,
轴对称,![]() 关于
关于![]() 轴对称.
轴对称.
令 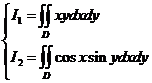 ,
,
由于![]() 对
对![]() 及对
及对![]() 都是奇函数,所以
都是奇函数,所以
![]() .
.
而![]() 对
对![]() 是偶函数,对
是偶函数,对![]() 是奇函数,故有
是奇函数,故有
![]() ,
,
所以 ![]() ,
,
故选(A).
(5)【答案】(D)
【解析】矩阵的乘法公式没有交换律,只有一些特殊情况可以交换.
由于![]() 、
、![]() 、
、![]() 均为
均为![]() 阶矩阵,且
阶矩阵,且![]() ,对等式两边取行列式,据行列式乘法公式
,对等式两边取行列式,据行列式乘法公式
![]() ,得到
,得到![]() 、
、![]() 、
、![]() ,知
,知![]() 、
、![]() 、
、![]() 均可逆,那么,对于
均可逆,那么,对于![]() ,先左乘
,先左乘![]() 再右乘
再右乘![]() 有
有 ![]() ,故应选(D).
,故应选(D).
其实,对于![]() 先右乘
先右乘![]() 再左乘
再左乘![]() ,有
,有![]() .
.
三、(本题满分15分,每小题5分.)
(1)【解析】这是![]() 型未定式求极
型未定式求极