时间:2016-03-05 17:17:24
【解析】由题意可得:
![]()
![]()
因为:![]() 所以
所以![]()
(17)(本题满分10分)
设平面内区域![]() 由直线
由直线![]() 及
及![]() 围成.计算
围成.计算![]() 。
。
【解析】![]()
![]()
![]()
(18)(本题满分10分)
设奇函数![]() 在
在![]() 上具有二阶导数,且
上具有二阶导数,且![]() .证明:
.证明:
(I)存在![]() ,使得
,使得![]() ;(II)存在
;(II)存在![]() ,使得
,使得![]() 。
。
【解析】(1)令![]()
则![]() 使得
使得![]()
(2)令![]() 则
则![]()
又由于![]() 为奇函数,故
为奇函数,故![]() 为偶函数,可知
为偶函数,可知![]() ,
,
则![]() 使
使![]()
即![]() ,即
,即![]()
(19)(本题满分11分)
求曲线![]() 上的点到坐标原点的最长距离与最短距离。
上的点到坐标原点的最长距离与最短距离。
【解析】本题本质上是在条件![]() 下求函数
下求函数![]() 的最值。
的最值。
故只需求出![]() 在条件
在条件![]() 下的条件极值点,再将其与曲线端点处(
下的条件极值点,再将其与曲线端点处(![]() )的函数值比较,即可得出最大值与最小值。
)的函数值比较,即可得出最大值与最小值。
由于函数![]() 与
与![]() 的增减性一致,故可以转化为求
的增减性一致,故可以转化为求![]() 的条件极值点:
的条件极值点:
构造拉格朗日函数![]() ,求其驻点得
,求其驻点得
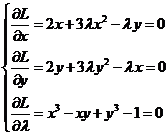
为了求解该方程组,将前两个方程变形为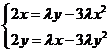
进一步有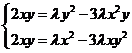 ,故
,故![]()
即![]() 。则有
。则有![]() 或
或![]() 或
或![]() 。
。
当![]() 时,有
时,有![]() ,不可能满足方程
,不可能满足方程![]() ;
;
当![]() ,由于
,由于![]() ,也只能有
,也只能有![]() ,不可能满足第三个方程;
,不可能满足第三个方程;
故必有![]() ,将其代入
,将其代入![]() 得
得![]() ,解得
,解得![]() 。
。
可知![]() 点是唯一的条件极值点。
点是唯一的条件极值点。
由于![]() ,
,![]() ,故曲线
,故曲线![]() 上的点到坐标原点的最长距离为
上的点到坐标原点的最长距离为![]() 与最短距离为
与最短距离为![]() 。
。
(20)(本题满分11分)
设函数![]() ,
,
(I)求![]() 的最小值
的最小值
(II)设数列![]() 满足
满足![]() ,证明
,证明![]() 存在,并求此极限.
存在,并求此极限.
【解析】(I)![]() ,则当
,则当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() 。
。
可知![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增。故
上单调递增。故![]() 的最小值为
的最小值为![]() 。
。
(2)、由于![]() ,则
,则![]() ,即
,即![]() ,故
,故![]() 单调递增。
单调递增。
又由于![]() ,则
,则![]() ,故
,故![]() 有上界,则由单调有界收敛定理可知,
有上界,则由单调有界收敛定理可知,![]() 存在。令
存在。令![]() ,则
,则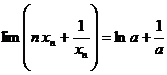 ,由于
,由于![]() ,则
,则
![]() ,故
,故![]() 。
。
(21)(本题满分11分)
设曲线![]() 的方程为
的方程为![]() ,
,
(1)求![]() 的弧长;
的弧长;
(2)设![]() 是由曲线
是由曲线![]() ,直线
,直线![]() 及
及![]() 轴所围平面图形,求
轴所围平面图形,求![]() 的形心的横坐标。
的形心的横坐标。
【解析】(1)由弧长的计算公式得![]() 的弧长为
的弧长为
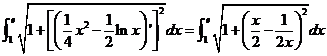
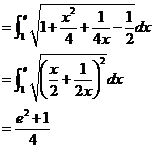
(2)由形心的计算公式可得,![]() 的形心的横坐标为
的形心的横坐标为
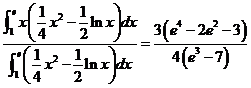
(22)(本题满分11分)
设![]() ,当
,当![]() 为何值时,存在矩阵
为何值时,存在矩阵![]() 使得
使得![]() ,并求所有矩阵
,并求所有矩阵![]() 。
。
【解析】由题意可知矩阵C为2阶矩阵,故可设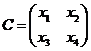 ,则由
,则由![]() 可得线性方程组:
可得线性方程组:
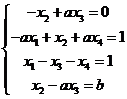 (1)
(1)
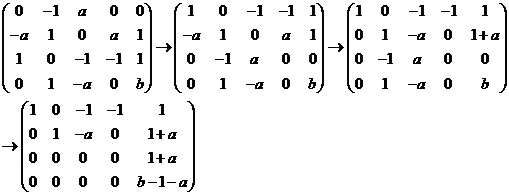
由于方程组(1)有解,故有![]() ,即
,即![]() 从而有
从而有
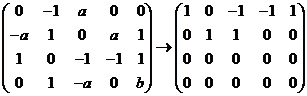 ,故有
,故有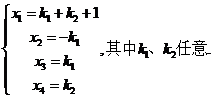
从而有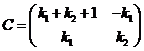
(23)(本题满分11分)
设二次型![]() ,记
,记 。
。
(I)证明二次型![]() 对应的矩阵为
对应的矩阵为![]() ;
;
(II)若![]() 正交且均为单位向量,证明二次型
正交且均为单位向量,证明二次型![]() 在正交变化下的标准形为二次型
在正交变化下的标准形为二次型![]() 。
。
【解析】(1)
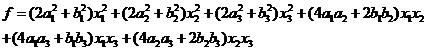
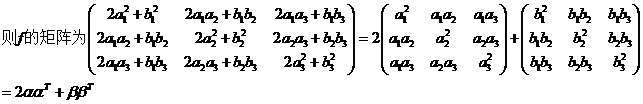 (2)
(2)![]() ,则1,2均为A的特征值,又由于
,则1,2均为A的特征值,又由于![]() ,故0为A的特征值,则三阶矩阵A的特征值为2,1,0,故f在正交变换下的标准形为
,故0为A的特征值,则三阶矩阵A的特征值为2,1,0,故f在正交变换下的标准形为![]()