时间:2016-03-05 16:45:18
【详解】 方法一:任一原函数可表示为![]() ,且
,且![]()
当F(x)为偶函数时,有![]() ,于是
,于是![]() ,即
,即 ![]() ,也即
,也即![]() ,可见f(x)为奇函数;反过来,若f(x)为奇函数,则
,可见f(x)为奇函数;反过来,若f(x)为奇函数,则![]() 为偶函数,从而
为偶函数,从而![]() 为偶函数,可见(A)为正确选项.
为偶函数,可见(A)为正确选项.
方法二:令f(x)=1, 则取F(x)=x+1, 排除(B)、(C); 令f(x)=x, 则取F(x)=![]() , 排除(D); 故应选(A).
, 排除(D); 故应选(A).
【评注】 函数f(x)与其原函数F(x)的奇偶性、周期性和单调性已多次考查过. 请读者思考f(x)与其原函数F(x)的有界性之间有何关系?
完全类似例题见《数学复习指南》(理工类)P.10【例1.5~1.7】
9..【分析】 先由x=3确定t的取值,进而求出在此点的导数及相应的法线方程,从而可得所需的横坐标.
【详解】 当x=3时,有![]() ,得
,得![]() (舍去,此时y无意义),于是
(舍去,此时y无意义),于是
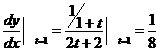 ,可见过点x=3(此时y=ln2)的法线方程为:
,可见过点x=3(此时y=ln2)的法线方程为:
![]() ,
,
令y=0, 得其与x轴交点的横坐标为:![]() , 故应(A).
, 故应(A).
【评注】注意本题法线的斜率应为-8. 此类问题没有本质困难,但在计算过程中应特别小心,稍不注意答案就可能出错.
完全类似例题见《数学复习指南》(理工类)P.53【例2.9】
10…【分析】 由于未知f(x)的具体形式,直接化为用极坐标计算显然是困难的. 本题可考虑用轮换对称性.
【详解】 由轮换对称性,有

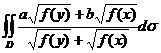
=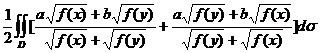
=![]() 应选(D).
应选(D).
【评注】 被积函数含有抽象函数时,一般考虑用对称性分析. 特别,当具有轮换对称性(x,y互换,D保持不变)时,往往用如下方法:
![]()
公式见P.285, 完全类似方法见《数学复习指南》(理工类)P.300【例11.26】
11…【分析】 先分别求出![]() 、
、![]() 、
、![]() ,再比较答案即可.
,再比较答案即可.
【详解】 因为![]() ,
,
![]() ,
,
于是 ![]() ,
,
![]() ,
,
![]() ,
,
可见有![]() ,应选(B).
,应选(B).
【评注】 本题综合考查了复合函数求偏导和隐函数求偏导以及高阶偏导的计算。作为做题技巧,也可取![]() ,则
,则![]() ,容易验算只有
,容易验算只有![]() 成立,同样可找到正确选项(B).
成立,同样可找到正确选项(B).
完全类似例题见《数学复习指南》(理工类)P.267【例10.16】及习题十(第11题)
12….
【分析】 显然x=0,x=1为间断点,其分类主要考虑左右极限.
【详解】 由于函数f(x)在x=0,x=1点处无定义,因此是间断点.
且 ![]() ,所以x=0为第二类间断点;
,所以x=0为第二类间断点;
![]() ,
,![]() ,所以x=1为第一类间断点,故应选(D).
,所以x=1为第一类间断点,故应选(D).
【评注】 应特别注意:![]() ,
,![]() 从而
从而![]() ,
,![]()
完全类似例题见《数学复习指南》(理工类)P.41【例1.68】
13….【分析】 讨论一组抽象向量的线性无关性,可用定义或转化为求其秩即可.
【详解】 方法一:令 ![]() ,则
,则
![]() ,
, ![]() .
.
由于![]() 线性无关,于是有
线性无关,于是有
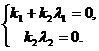
当![]() 时,显然有
时,显然有![]() ,此时
,此时![]() ,
,![]() 线性无关;反过来,若
线性无关;反过来,若![]() ,
,![]() 线性无关,则必然有
线性无关,则必然有![]() (,否则,
(,否则,![]() 与
与![]() =
=![]() 线性相关),故应选(B).
线性相关),故应选(B).
方法二: 由于 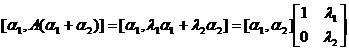 ,
,
可见![]() ,
,![]() 线性无关的充要条件是
线性无关的充要条件是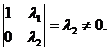 故应选(B).
故应选(B).
【评注】 本题综合考查了特征值、特征向量和线性相关与线性无关的概念.
完全类似例题见《数学复习指南》(理工类)P.407【例3.17】
14…【分析】 本题考查初等变换的概念与初等矩阵的性质,只需利用初等变换与初等矩阵的关系以及伴随矩阵的性质进行分析即可.
【详解】 由题设,存在初等矩阵![]() (交换n阶单位矩阵的第1行与第2行所得),使得
(交换n阶单位矩阵的第1行与第2行所得),使得 ![]() ,于是
,于是 ![]() ,即
,即
![]() ,可见应选(C).
,可见应选(C).
【评注】 注意伴随矩阵的运算性质:
![]() ,当A可逆时,
,当A可逆时,![]()
![]() .
.
完全类似例题及性质见《数学复习指南》(理工类)P.381【例2.14,例2.29】
15… 【分析】 此类未定式极限,典型方法是用洛必塔法则,但分子分母求导前应先变形.
【详解】 由于![]() ,于是
,于是
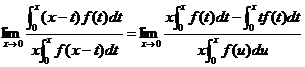
=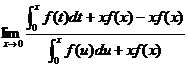 =
=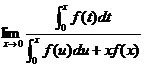
=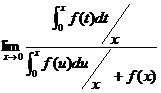 =
=![]()
【评注】 本题容易出现的错误是:在利用一次洛必塔法则后,继续用洛必塔法则
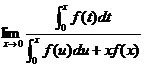 =
=![]()
错误的原因:f(x)未必可导.
完全类似处理方法见《数学复习指南》(理工类)P.5【例10】
16…. 【分析】 利用定积分的几何意义可确定面积![]() ,再根据
,再根据![]() 建立积分等式,然后求导引出微分方程,最终可得所需函数关系.
建立积分等式,然后求导引出微分方程,最终可得所需函数关系.
【详解】 如图,有
![]() ,
,
![]() ,
,
由题设,得 ![]() ,
,
而![]() ,于是
,于是![]()
两边对y求导得 ![]() ,
,
故所求的函数关系为:![]()
【评注】 本题应注意点M(x,y)在曲线![]() 上,因此满足
上,因此满足![]() .
.
17……【分析】 题设图形相当于已知f(x)在x=0的函数值与导数值,在x=3处的函数值及一阶、二阶导数值.
【详解】 由题设图形知,f(0)=0, ![]() ; f(3)=2,
; f(3)=2, ![]()
由分部积分,知
![]()
=![]()
=![]()
【评注】 本题f(x) 在两个端点的函数值及导数值通过几何图形给出,题型比较新颖,综合考查了导数的几何意义和定积分的计算. 另外,值得注意的是,当被积函数含有抽象函数的导数时,一般优先考虑用分部积分.
完全类似例题见《数学复习指南》(理工类)P.118【例4.36,4.30】
18…….【分析】 先将![]() 转化为
转化为![]() ,再用二阶常系数线性微分方程的方法求解即可.
,再用二阶常系数线性微分方程的方法求解即可.
【详解】 ![]() ,
,
![]() ,
,
代入原方程,得 ![]() .
.
解此微分方程,得 ![]() ,
,
将初始条件![]() 代入,有
代入,有![]() . 故满足条件的特解为
. 故满足条件的特解为![]()
【评注】 本题的关键是将![]() 转化为
转化为![]() ,而这主要是考查复合函数求一、二阶导数.
,而这主要是考查复合函数求一、二阶导数.
完全类似例题见《数学复习指南》(理工类)P.52【例2.8】
19….【分析】 第一部分显然用闭区间上连续函数的介值定理;第二部分为双介值问题,可考虑用拉格朗日中值定理,但应注意利用第一部分已得结论.
【详解】 (I) 令![]() ,则F(x)在[0,1]上连续,且F(0)=-1<0, F(1)=1>0,于是由介值定理知,存在存在
,则F(x)在[0,1]上连续,且F(0)=-1<0, F(1)=1>0,于是由介值定理知,存在存在![]() 使得
使得![]() ,即
,即![]() .
.
(II) 在![]() 和
和![]() 上对f(x)分别应用拉格朗日中值定理,知存在两个不同的点
上对f(x)分别应用拉格朗日中值定理,知存在两个不同的点![]() ,使得
,使得![]() ,
,![]()
于是 ![]()
【评注】 中值定理的证明问题是历年出题频率最高的部分,而将中值定理与介值定理或积分中值定理结合起来命题又是最常见的命题形式.
完全类似例题见《数学复习指南》(理工类)P.128【例5.4】,P.151【例5.25】
20……【分析】 根据全微分和初始条件可先确定f(x,y)的表达式. 而f(x,y)在椭圆域上的最大值和最小值, 可能在区域的内部达到,也可能在区域的边界上达到,且在边界上的最值又转化为求条件极值.
.【详解】 由题设,知 ![]() ,
,![]() ,
,
于是 ![]() ,且
,且 ![]() ,从而
,从而 ![]() ,
,
再由f(1,1)=2,得 C=2, 故 ![]()
令![]() 得可能极值点为x=0,y=0. 且
得可能极值点为x=0,y=0. 且 ![]() ,
,![]() ,
,![]() ,
,
![]() ,所以点(0,0) 不是极值点,从而也非最值点.
,所以点(0,0) 不是极值点,从而也非最值点.
再考虑其在边界曲线![]() 上的情形:令拉格朗日函数为
上的情形:令拉格朗日函数为
![]() ,
,
解 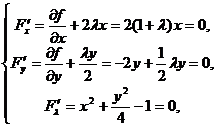
得可能极值点![]() ;
;![]() ;
;![]() ;
;![]() 代入f(x,y)得
代入f(x,y)得![]()
![]() ,可见z=f(x,y)在区域
,可见z=f(x,y)在区域 内的最大值为3,最小值为-2.
内的最大值为3,最小值为-2.
【评注】 本题综合考查了多元函数微分学的知识,涉及到多个重要基础概念,特别是通过偏导数反求函数关系,要求考生真正理解并掌握了相关知识.
完全类似例题见《数学复习指南》(理工类)P.279【例10.33】
21…..【分析】 被积函数含有绝对值,应当作分区域函数看待,利用积分的可加性分区域积分即可.
【详解】 记![]() ,
,
![]() ,
,
于是 ![]() =
=![]()
![]()
=![]()
![]()
![]()
=![]() +
+![]() =
=![]()
【评注】 形如积分![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 等的被积函数均应当作分区域函数看待,利用积分的可加性分区域积分.
等的被积函数均应当作分区域函数看待,利用积分的可加性分区域积分.
完全类似例题见《数学复习指南》(理工类)P.295【例11.16】
22……【分析】向量组![]() 可由向量组
可由向量组![]() 线性表示,相当与方程组:
线性表示,相当与方程组:
![]() .
.
均有解,问题转化为![]() =
=![]() 是否均成立?这通过初等变换化解体形讨论即可. 而向量组
是否均成立?这通过初等变换化解体形讨论即可. 而向量组![]() 不能由向量组
不能由向量组![]() 线性表示,相当于至少有一个向量
线性表示,相当于至少有一个向量![]() 不能由
不能由![]() 表示,即至少有一方程组
表示,即至少有一方程组
![]() ,无解.
,无解.
【详解】 对矩阵![]() 作初等行变换,有
作初等行变换,有
![]() =
=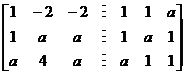
![]()
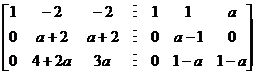
![]()
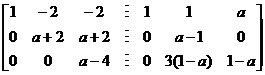 ,
,
当a=-2时,![]()
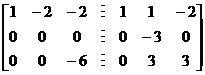 , 显然
, 显然![]() 不能由
不能由![]() 线性表示,因此
线性表示,因此![]() ;当a=4时,
;当a=4时,
![]()
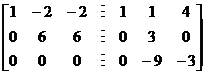 ,然
,然![]() 均不能由
均不能由![]() 线性表示,因此
线性表示,因此![]() .
.
而当![]() 且
且![]() 时,秩
时,秩![]() ,此时向量组
,此时向量组![]() 可由向量组
可由向量组![]() 线性表示.
线性表示.
又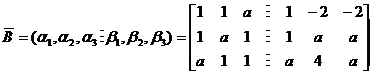
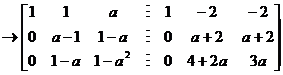
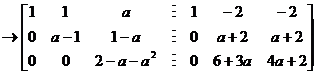 ,
,
由题设向量组![]() 不能由向量组
不能由向量组![]() 线性表示,必有
线性表示,必有![]() 或
或![]() ,即a=1或
,即a=1或![]() .
.
综上所述,满足题设条件的a只能是:a=1.
【评注】 1)向量组![]() 不能由向量组
不能由向量组![]() 线性表示,必有行列式:
线性表示,必有行列式:
![]() ,由此也可确定a .
,由此也可确定a .
2) 向量