时间:2016-03-05 16:31:10
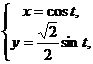
![]()
故 ![]() ,
,
令![]() ,则
,则
![]()
=![]()
【评注】 注意只在第一象限考虑曲线y=f(x)的弧长,所以积分限应从0到![]() ,而不是从0到
,而不是从0到![]()
【详解】 (1) 设在t时刻,液面的高度为y,则由题设知此时液面的面积为![]() , 从而
, 从而 ![]()
(2) 液面的高度为y时,液体的体积为![]()
上式两边对y求导,得
![]() ,即
,即 ![]()
解此微分方程,得
![]() ,其中C为任意常数,
,其中C为任意常数,
由![]() 知C=2,
知C=2,
故所求曲线方程为
![]()
【评注】 作为应用题,本题比较好地综合考查了定积分在几何上的应用与微分方程的求解。
十.. 【分析】 (1) 由![]() 存在知,f(a)=0, 利用单调性即可证明f(x)>0. (2) 要证的结论显含f(a),f(b),应将要证的结论写为拉格朗日中值定理或柯西中值定理的形式进行证明. (3) 注意利用(2)的结论证明即可.
存在知,f(a)=0, 利用单调性即可证明f(x)>0. (2) 要证的结论显含f(a),f(b),应将要证的结论写为拉格朗日中值定理或柯西中值定理的形式进行证明. (3) 注意利用(2)的结论证明即可.
【详解】 (1) 因为![]() 存在,故
存在,故![]() 又
又![]() ,于是f(x)在(a,b)内单调增加,故
,于是f(x)在(a,b)内单调增加,故
![]()
(2) 设F(x)=![]() ,
,![]() , 则
, 则![]() ,故
,故![]() 满足柯西中值定理的条件,于是在(a,b)内存在点
满足柯西中值定理的条件,于是在(a,b)内存在点![]() ,使
,使
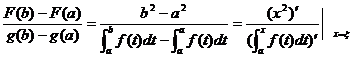 ,
,
即  .
.
(3) 因![]() ,在
,在![]() 上应用拉格朗日中值定理,知在
上应用拉格朗日中值定理,知在![]() 内存在一点
内存在一点![]() ,使
,使![]() ,从而由(2) 的结论得
,从而由(2) 的结论得
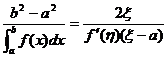 ,
,
即有 ![]()
【评注】 证明(3),关键是用(2)的结论:
![]()
![]()
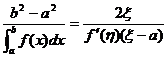
![]() ( 根据(2) 结论 )
( 根据(2) 结论 )
![]() ,
,
可见对f(x)在区间![]() 上应用拉格朗日中值定理即可.
上应用拉格朗日中值定理即可.
十一。 【分析】 已知A相似于对角矩阵,应先求出A的特征值,再根据特征值的重数与线性无关特征向量的个数相同,转化为特征矩阵的秩,进而确定参数a. 至于求P,则是常识问题.
【详解】 矩阵A的特征多项式为
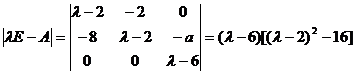
=![]() ,
,
故A的特征值为![]()
由于A相似于对角矩阵![]() ,故对应
,故对应![]() 应有两个线性无关的特征向量,即
应有两个线性无关的特征向量,即
![]() ,于是有
,于是有 ![]()
由 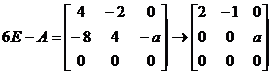 ,
,
知a=0.
于是对应于![]() 的两个线性无关的特征向量可取为
的两个线性无关的特征向量可取为
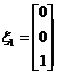 ,
, 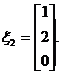
当![]() 时,
时,
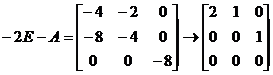 ,
,
解方程组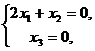 得对应于
得对应于![]() 的特征向量
的特征向量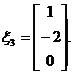
令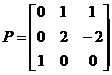 ,则P可逆,并有
,则P可逆,并有![]()
十二。 【分析】 三条直线相交于一点,相当于对应线性方程组有唯一解,进而转化为系数矩阵与增广矩阵的秩均为2.
【详解】 方法一:必要性
设三条直线![]() 交于一点,则线性方程组
交于一点,则线性方程组
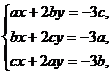 (*)
(*)
有唯一解,故系数矩阵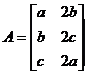 与增广矩阵
与增广矩阵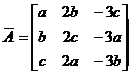 的秩均为2,于是
的秩均为2,于是![]()
由于 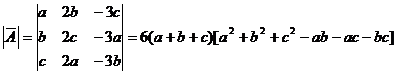
=![]() ,
,
但根据题设 ![]() ,故
,故
![]()
充分性:由![]() ,则从必要性的证明可知,
,则从必要性的证明可知,![]() ,故秩
,故秩![]()
由于
![]()
=![]() ,
,
故秩(A)=2. 于是,
秩(A)=秩![]() =2.
=2.
因此方程组(*)有唯一解,即三直线![]() 交于一点.
交于一点.
方法二:必要性
设三直线交于一点![]() ,则
,则![]() 为Ax=0的非零解,其中
为Ax=0的非零解,其中
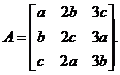
于是 ![]() .
.
而 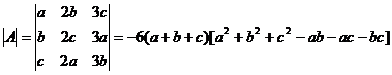
=![]() ,
,
但根据题设 ![]() ,故
,故
![]()
充分性:考虑线性方程组
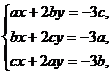 (*)
(*)
将方程组(*)的三个方程相加,并由a+b+c=0可知,方程组(*)等价于方程组
![]() (* *)
(* *)
因为 ![]()
=-![]() ,
,
故方程组(* *)有唯一解,所以方程组(*)有唯一解,即三直线![]() 交于一点.
交于一点.
【评注】本题将三条直线的位置关系转化为方程组的解的判定,而解的判定问题又可转化为矩阵的秩计算,进而转化为行列式的计算,综合考查了多个知识点.