时间:2012-11-29 23:24:44
行程问题第三讲
两个速度不同的人或车,慢的先行(领先)一段,然后快的去追,经过一段时间快的追上慢的。这样的问题一般称为追及问题。有时,快的与慢的从同一地点同时出发,同向而行,经过一段时间快的领先一段路程,我们也把它看作追及问题,因为这两种情况都满足
速度差×时间=追及(或领先的)路程
对于有三个以上人或车同时参与运动的行程问题,在分析其中某两个的运动情况的同时,还要弄清此时此刻另外的人或车处于什么位置,他(它)与前两者有什么关系。
分析复杂的行程问题时,最好画线段图帮助思考
理解并熟记下面的结论,对分析、解答复杂的行程问题是有好处的。
(1) 如果甲的速度是乙的a倍(或b/a),那么,在相同时间内,甲所行的路程也是乙的a倍(或b/a);
(2) 如果甲的速度是乙的a倍(或b/a),那么,行完同样的路程,乙所用的时间是甲的a倍(或b/a);
(3) 甲的速度是a,乙的速度是b,在相同时间内,甲、乙一共行的路程为S,那么,其中甲所行的路程为[a/(a+b)] ×S,乙所行的路程为[b/(a+b)] ×S
【例1】甲、乙两人分别从A、B两地同时出发,相向而行。如果两人都按原定速度行进,那么4小时相遇;现在两人都比原计划每小时少走
【分析】可以想象,如果甲、乙两人以现在的速度(比原计划每小时少走
【解】1×4×2÷(5-4)×5=40(千米)
这道题属于相遇问题,它的基本关系式是:速度和×时间=(相隔的)路程。但只有符合“同时出发,相向而行,经过相同时间相遇”这样的特点才能运用上面的关系式。不过,当出现“不同时出发”或“没有相遇(而是还相隔一段路)”的情况时,应该通过转化条件,然后应用上面的关系式。
【例2】小王、小张步行的速度分别是每小时4
【分析】为便于分析,画出线段图36-1:
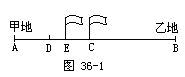
图中C点表示小张与小李相遇地点,D点表示他们相遇时小王所在地点。
根据题意,小王从D点、小李从C点同时出发,相向而行,经过5分钟相遇。因此,DC的长为
(4.8+10.8)×(5/60)=1.3(千米)
这段长度也是相同时间内,小张比小王多行的路程。这里的“相同时间”指从三人同时出发到小张与小李相遇所经过的时间。这段时间为
1.3÷(5.4-4.8)×60=130(分)
这就是说,小张行完AC这段路(也就是小李行完CB这段路)用了130分钟,而小李的速度是小张速度的2(=10.8÷5.4)倍,所以小李行完AC这段路只需小张的一半时间(65分)。
【解】(留给读者完成,答案是195分钟。)
【例3】上午8点8分,小明骑自行车从家里出发, 8分钟后,爸爸骑摩托车去追他,在离家
【分析】先画出示意图图37-1如下(图37-1中A点表示爸爸第一次追上小明的地方,B点表示他第二次追上小明的地方)。从图37-1上看出,在相同时间(从第一次追上到第二次追上)内,小明从A点到B点,行完(8-4=)
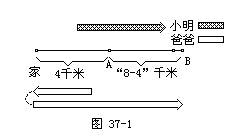
由于小明从家出发8分钟后爸爸去追他,并且在A点追上,所以,小明从家到A点比爸爸多用8分钟。这样可以算出,小明从家到A所用的时间为
8÷(3-1)×3=12(分)
【解】8÷(3-1)×3×X2=24(分)
【例4】甲、乙两车分别从A、B两地同时出发,相向而行。甲车每小时行
【分析】我们同样还是画出示意图 37-2(图 37-2中P、M、N分别为第一次、第二次、第三次相遇地点):
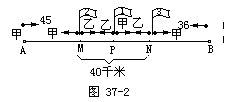
设 AB两地的距离为“1”。由甲、乙两车的速度可以推知:在相同时间内,乙车所行的路程是甲车所行路程的(4/5)=(36/45)。从而,甲乙两车所行的路程分别占他们共同完成路程的(5/9)=(5/(4+5))和(4/9)=(5/(4+5))
通过演示我们还可以知道,第二次相遇时,甲、乙两车一共行完了3个全程(AB+BM+BA+AM);第三次相遇时,它们一共行完了5个全程(AB+BA+AN+BA+AB+BN)。
下面,我们只要找出与“40千米”相对应的分率(也就是MN占全程的几分之几)。
【解】
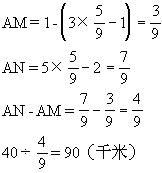
注意:为了保证计算正确,应当在示意图中标上三次相遇时甲、乙两车行的方向。
我们来讨论封闭线路的行程问题。
解决封闭路线中的行程问题,仍要抓住“路程=速度×时间”这个基本关系式,搞清路程、速度、时间三者之间的关系。
封闭路线中的行程问题,可以转化为非封闭路线中的行程问题来解决。在求两个沿封闭路线相向运动的人或物体相遇次数时,还可以借助图示直观地解决。
直线上的来回运动、钟表上的时针分针夹角问题,实质上也是封闭路线中的行程问题。
[1] [2] [3] [4]