时间:2020-05-23 22:12:41
1、单选题 甲班有42名学生,乙班有48名学生。已知在某次数学考试中按百分制评卷,评卷结果各班的数学总成绩相同,各班的平均成绩都是整数,并且平均成绩都高于80分,那么甲班的平均成绩比乙班高多少分?_____
A: 10
B: 11
C: 12
D: 13
参考答案: C
本题解释:正确答案是C考点平均数问题解析解析1:设乙班学生的平均成绩为x分,甲班比乙班平均成绩高y分,则可得方程:42(x+y)=48x,x=7y。将选项分别代入等式,x分别等于70,77,84,91。根据已知条件各班平均成绩都高于80分,可排A、B项。将C、D项代入已知条件算出甲班的平均成绩分别为96、104,因为考试按百分制评卷,排除D。故本题正确答案为C。解析2:由题干总成绩相同,可知总成绩是42和48的公倍数。两个数的最小公倍数为336,所以总成绩是336的倍数,记作336n(n为整数),则平均分差异为336n÷42-336n÷48=n。又试卷为百分制,且平均分都高于80分,那么48×80<336n<42×100,故80/7标签直接代入数字特性
2、单选题 一副扑克牌有四种花色,每种花色各有13张,现在从中任意抽牌。问最少抽几张牌,才能保证有4张牌是同一种花色的?_____
A: 12
B: 13
C: 15
D: 16
参考答案: B
本题解释:正确答案是B解析如果没有4张同一花色的,最坏的情况就是每种都有3张了,也就是抽了12张牌的时候,还没有4张同色的。在最坏的基础上加一张牌,就一定会有4张牌是同一花色的了,此时是13张牌,故正确答案为B。抽屉原理问题
3、单选题 把12棵同样的松树和6棵同样的柏树种植在道路两侧,每侧种植9棵,要求每侧的柏树数量相等且不相邻,且道路起点和终点处两侧种植的都必须是松树。问有多少种不同的种植方法:_____
A: 36
B: 50
C: 100
D: 400
参考答案: C
本题解释:正确答案是C,解析:根据题意,道路起点和终点处两侧种植的都必须是松树,故只需要安排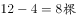
4、单选题 有40辆汽车,其中30%是货车,其余是轿车。如果有1/4的轿车是出租车,问不是出租车的轿车有几辆?_____
A: 7
B: 12
C: 18
D: 21
参考答案: D
本题解释:正确答案是D考点和差倍比问题解析由题意得:轿车的数量为40×(1-30%)=28(辆),则不是出租车的轿车数目为28×(1-1/4)=21(辆)。故正确答案为D。
5、单选题 某矿井发生透水事故,且矿井内每分钟涌出的水量相等,救援人员调来抽水机抽水,如果用两台抽水机抽水,预计40分钟可抽完;如果用4台同样的抽水机,16分钟可抽完。为赢得救援时间,要在10分钟内抽完矿井内的水,那么至少需要抽水机_____。
A: 5台
B: 6台
C: 7台
D: 8台
参考答案: B
本题解释:正确答案是B考点牛吃草问题解析解析1:假定矿井原有水量为N,每分钟涌入的水量为n,根据题意可得N=(2-n)×40,N=(4-n)×16,解得n=2/3,N=160/3,因此要在10分钟内抽完矿井内的水需要抽水机为160/3÷10+2/3=6台。公式:在牛吃草模型背景下,公式为N=(牛数-x)×天数,其中N表示原有草量的存量,以牛数与天数的乘积来衡量;x表示专门吃新增加草量所需要的牛数。解析2:设每台抽水机每分钟抽水1个单位,那么,每分钟进水量为(2×40-4×16)÷(40-16)=2/3个单位,原来的积水量为2×40-(2/3)×40=160/3,那么10分钟内抽完水,需要[(160/3)+10×(2/3)]÷10=6台。故正确答案为B。标签赋值思想