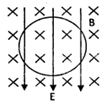
2、计算题  （18分）如图所示，真空中以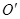为圆心，半径r=0.1m的圆形区域内只存在垂直纸面向外的匀强磁场，圆形区域的最下端与xoy坐标系的x轴相切于坐标原点O，圆形区域的右端与平行y轴的虚线MN相切，在虚线MN右侧x轴的上方足够大的范围内有方向水平向左的匀强电场，电场强度E=1.0×105 N/C。现从坐标原点O沿xoy平面在y轴两侧各30°角的范围内发射速率均为v0=1.0×106m/s的带正电粒子，粒子在磁场中的偏转半径也为r=0.1m，已知粒子的比荷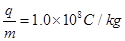，不计粒子的重力、粒子对电磁场的影响及粒子间的相互作用力，求：

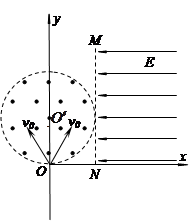
（1）磁场的磁感应强度B的大小；
（2）沿y轴正方向射入磁场的粒子，在磁场和电场中运动的总时间；
（3）若将匀强电场的方向改为竖直向下，其它条件不变，则粒子达到x轴的最远位置与最近位置的横坐标之差。

3、计算题  (18分) 如图所示，在足够大的空间范围内，同时存在着竖直向上的匀强电场和垂直纸面向外的匀强磁场，电场强度为E，磁感应强度为B．足够长的光滑斜面固定在水平面上，斜面倾角为30．有一带电的物体P静止于斜面顶端且P对斜面无压力，若给物体P一瞬时冲量，使其获得水平方向的初速度向右抛出，同时另有一不带电的物体Q从A处由静止开始沿斜面滑下（P、Q均可视为质点），P、Q二物体运动轨迹在同一竖直平面内．一段时间后，物体P恰好与斜面上的物体Q相遇，且相遇时物体P的速度方向与其水平初速度方向的夹角为60．已知重力加速度为，求：
（1）P、Q相遇所需的时间；
（2）物体P在斜面顶端受到瞬时冲量后所获得的初速度的大小．

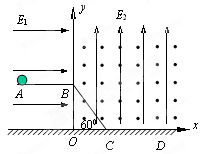
4、计算题  （16分）如图所示，坐标系xOy在竖直平面内，水平轨道AB和斜面BC均光滑且绝缘，AB和BC的长度均为L，斜面BC与水平地面间的夹角θ=600?，有一质量为m、电量为+q的带电小球（可看成质点）被放在A点。已知在第一象限分布着互相垂直的匀强电场和匀强磁场，电场方向竖直向上，场强大小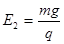，磁场为水平方向（图中垂直纸面向外），磁感应强度大小为B；在第二象限分布着沿x轴正向的水平匀强电场，场强大小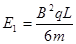。现将放在A点的带电小球由静止释放，则小球需经多少时间才能落到地面（小球所带的电量不变）？

5、选择题  一个带电粒子穿过某一空间而未发生偏转，则下列说法中正确的是
A．此空间一定不存在磁场
B．此空间可能有磁场，方向与电子的速度方向平行
C．此空间可能有磁场，方向与电子的速度方向垂直
D．此空间可能有正交的匀强电场和匀强磁场，它们的方向均与电子的速度方向垂直