时间:2017-08-09 09:01:44
1、计算题 如图所示,水平虚线L1.L2间的高度差h=5cm,L1的上方和L2的下方都存在垂直
纸面向里的匀强磁场和竖直向上的匀强电场,下方磁场的磁感应强度是上方的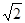 倍,一带
倍,一带
电微粒正好能在竖直平面内沿图中轨迹做周期性运动,在两磁场中的轨迹是半圆.当运动到
轨迹最低点时,如果撤去电场,微粒将做匀速直线运动.取g=10m/s2. 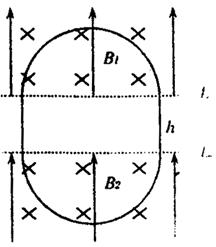
小题1:说出微粒的绕行方向;
小题2:分别求出微粒在两磁场中的速度大小;
参考答案:
小题1:粒子带正电,绕行方向为逆时针
小题2:v2=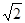 m/s
m/s
本题解析:(1)粒子带正电,绕行方向为逆时针……………………………3分
(2)设上、下半圆中的速度相磁感应强度分别为V1,V2,B1,B2
则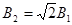 ?……………………………2分
?……………………………2分
qE=mg………………………………………………2分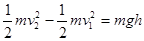 …………………………2分
…………………………2分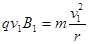 ……………………………………2分
……………………………………2分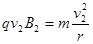 ………………………………………2分
………………………………………2分
解以上各式得v1="1m/s?" v2=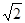 m/s……………………………2分
m/s……………………………2分
本题难度:一般
2、选择题 如图所示,a、b为竖直正对放置的平行金属板构成的偏转电场,其中a板带正电,两板间的电压为U,在金属板下方存在一有界的匀强磁场,磁场的上边界为与两金属板下端重合的水平面PQ,PQ下方的磁场范围足够大,磁场的磁感应强度大小为B,一比荷为带正电粒子以速度为v0从两板中间位置与a、b平等方向射入偏转电场,不计粒子重力,粒子通过偏转电场后从PQ边界上的M点进入磁场,运动一段时间后又从PQ边界上的N点射出磁场,设M、N两点距离为x(M、N点图中未画出)。则以下说法中正确的是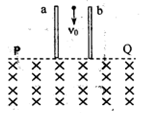
A.只减小磁感应强度B的大小,则x减小
B.只增大初速度v0的大小,则x减小
C.只减小偏转电场的电压U的大小,则x不变
D.只减小为带电粒子的比荷大小,则x不变
参考答案:C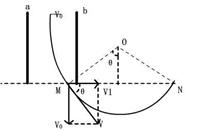
本题解析:粒子进入磁场时的速度为v=v0/sinθ,粒子在磁场中半径r=mv/qB,x=2rsinθ,解x=2mv0/qB,C正确。
本题难度:一般
3、选择题 如图所示,在平行金属板A、B间分布着正交的匀强电场和磁场,磁感应强度垂直纸面向里,一个质子以初速度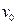 垂直于电磁场沿
垂直于电磁场沿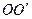 入射,恰能沿
入射,恰能沿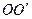 运动,则(?)
运动,则(?)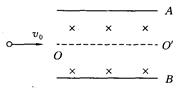
A.A板的电势高于B板的电势
B.电子以初速度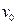 垂直于电磁场沿
垂直于电磁场沿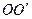 从左端入射,仍沿
从左端入射,仍沿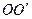 做直线运动
做直线运动
C. 以初速度
以初速度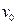 垂直于电磁场沿
垂直于电磁场沿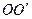 从左端入射,仍沿
从左端入射,仍沿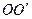 做直线运动
做直线运动
D. 以初速度
以初速度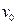 垂直于电磁场沿
垂直于电磁场沿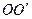 从右端入射,仍沿
从右端入射,仍沿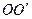 做直线运动
做直线运动
参考答案:ABC
本题解析:由于质子做匀速直线运动,所以电场力与洛伦兹力平衡。由左手定则知洛伦兹力向上,所以电场力向下,A板电势高,B板电势低,A对。由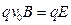 知,只要
知,只要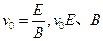 三者的方向符合右手定则,不论粒子的电荷量如何,均能做匀速直线运动,B、C均对,D错。
三者的方向符合右手定则,不论粒子的电荷量如何,均能做匀速直线运动,B、C均对,D错。
本题难度:一般
4、选择题 在空间某一匀强电场中,将一质量为m.电荷量为q的小球由静止释放.带电小球 的运动轨迹为一直线.该直线与竖直方向成锐角 ,电场强度大小为E。则下列说法中正确的足
,电场强度大小为E。则下列说法中正确的足
A.由于小球所受的电场力和重力做功均与路径无关.故小球的机械能守恒
B.若 ,则小球的电势能不变.机械能守恒
,则小球的电势能不变.机械能守恒
c.若 且
且 -则小球的动能必增大,电势能可能增大
-则小球的动能必增大,电势能可能增大
D.若 且
且 .则小球的动能必增大.电势能可能增大
.则小球的动能必增大.电势能可能增大
参考答案:BD
本题解析:小球受到电场力和重力作用,只有重力做功时机械能才平衡,但是电场力是否做功不确定,所以无法判断机械能是否守恒选项A错。物体从静止开始做直线运动,所以重力和电场力的合力与速度同向,若 ,则电场力
,则电场力 ,受力分析如下图左图,此时电场力和合力方向即运动方向垂直,电场力不做功,电势能不变,只有重力做功,机械能守恒。选项B对。若
,受力分析如下图左图,此时电场力和合力方向即运动方向垂直,电场力不做功,电势能不变,只有重力做功,机械能守恒。选项B对。若 ,则有电场力
,则有电场力 ,若
,若 此时受力分析如下右图,电场力只能水平向左如图,此时合力与速度同向,动能必然增大,电场力做正功,电势能一定减少选项C错。若
此时受力分析如下右图,电场力只能水平向左如图,此时合力与速度同向,动能必然增大,电场力做正功,电势能一定减少选项C错。若 电场力可能水平也可能斜向上如图,此时合力仍然与速度垂直,做正功,动能增大,电场力做负功, 电势能减少,所以电势能可能增大也可能减少选项D对。
电场力可能水平也可能斜向上如图,此时合力仍然与速度垂直,做正功,动能增大,电场力做负功, 电势能减少,所以电势能可能增大也可能减少选项D对。

本题难度:一般
5、填空题 如图所示,a、b、c、d四种离子,它们带等量同种电荷,质量为ma=mb<mc=md,以不等的速率va<vb=vc<vd进入速度选择器后,有两种离子从选择器中射出,进入磁感应强度为B2的磁场.由此可以判断射向D1的是_________离子.(不计重力)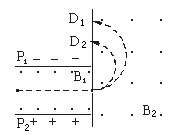
参考答案:C
本题解析:从速度选择器中射出的粒子,一定是速度相等的bc粒子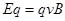 ,进入B2的磁场粒子做匀速圆周运动的轨迹半径
,进入B2的磁场粒子做匀速圆周运动的轨迹半径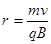 因为两粒子vqB都相同可知质量大半径大,即判断射向D1的是c粒子
因为两粒子vqB都相同可知质量大半径大,即判断射向D1的是c粒子
本题难度:简单