时间:2017-08-09 08:29:55
1、计算题 (12分)一同学想设计一个轨道玩具,其设想是将一光滑的倾角为θ斜面轨道和一半径为r的光滑半圆弧轨道两轨道平滑无缝连接,半圆弧轨道最高点和最低点在同一竖直线上,在轨道连接处无能量损失,让一小球从斜面上某一位置由静止释放,沿斜面轨道和半圆弧轨道运动,经过圆弧的顶点水平抛出并垂直落在斜面上,如图所示,如果他的想法可行,则斜面倾角θ应满足什么条件?在满足条件的情况下,小球释放位置距斜面底端高h为? 
参考答案: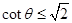 或
或 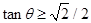 ?
?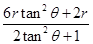
本题解析:设小球从圆弧顶点以速度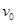 抛出,经过时间秒垂直落在斜面上,斜面的倾角为
抛出,经过时间秒垂直落在斜面上,斜面的倾角为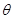 .如图所示
.如图所示
则: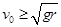 ?(1分)
?(1分)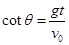 ?(1分)
?(1分)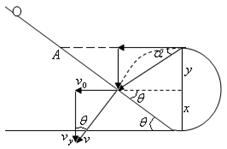
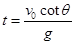 ?(1分)
?(1分)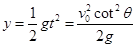 ?(1分)
?(1分)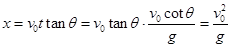 ?(1分)
?(1分)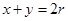 ?(1分)?
?(1分)?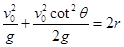 ?
?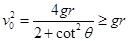 ?或
?或 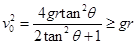 ?(1分)
?(1分)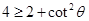 ?即:
?即: 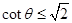 ?或
?或 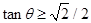 ?(1分)
?(1分)
所以,当斜面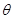 角满足
角满足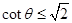 或
或 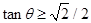 时,其设计是可行的.
时,其设计是可行的.
当小球在斜面上运动到与圆弧顶端等高位置A点时,小球的速度为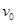 .
.
设此时小球下落高度为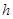 ,根据动能定理,
,根据动能定理,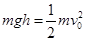 ?(1分)
?(1分)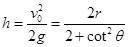 ?
?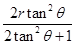 ?(1分)
?(1分)
所以,小球下滑的高度距斜面底端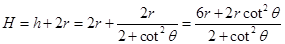
或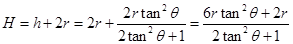 ?(2分)
?(2分)
本题难度:一般
2、选择题 下列关于运动物体所受合外力做功和动能变化的关系正确的是( )
A.如果物体所受合外力为零,则合外力对物体做的功一定为零
B.如果合外力对物体所做的功为零,则合外力一定为零
C.物体在合外力作用下做变速运动,动能一定发生变化
D.物体的动能不变,所受合外力一定为零
参考答案:
A、如果物体所受合外力为零,根据功的公式W=Flcosα得知,合外力对物体做的功一定为零.故A正确.
B、如果合外力做的功为零,但合外力不一定为零,也可能物体的合外力和运动方向垂直而不做功,比如匀速圆周运动.故B错误.
C、物体做变速运动可能是速度方向变化而速度大小不变.所以,做变速运动的物体,动能可能不变,故C错误.
D、物体动能不变,根据动能定理得知,合外力不做功,但合外力不一定为零.故D错误.
故选A
本题解析:
本题难度:简单
3、选择题 如图,质量为M的物体从地面上方H处无初速释放,落在地面后出现一个深为h的坑,在此过程中( )
A.重力对物体做功MgH
B.物体重力势能减少MgH
C.合力对物体做的总功为零
D.外力对物体做功Mg(H+h)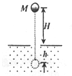
参考答案:A、根据重力做功的公式可知:WG=Mg△h=Mg(H+h).故A错误.
B、重力做的功为Mg(H+h),且为正功,则物体重力势能减少Mg(H+h).故B错误.
C、对整个过程运用动能定理得:W总=△EK=0,故C正确.
D、对整个过程运用动能定理得:外力对物体做功W总=WG+(-fh)=△EK=0.故D错误.
故选C
本题解析:
本题难度:简单
4、选择题 如图所示,DO是水平面,AB是斜面,初速度为vo的物体从D点出发沿DBA滑到顶点A时速度刚好为零.如果斜面改为AC,让该物体从D点出发沿DCA滑动到A点且速度刚好为零,则物体具有的初速度(已知物体与路面间的动摩擦因数处处相同且不为零且转弯处无能量损失)( )
A.大于vo
B.等于vo
C.小于vo
D.取决于斜面的倾角
参考答案:物体从D点滑动到顶点A过程中
-mg?xAO-μmg?xDB-μmgcosα?xAB=-12mv2
由几何关系cosα?xAB=xOB,因而上式可以简化为
-mg?xAO-μmg?xDB-μmg?xOB=-12mv2
-mg?xAO-μmg?xDO=-12mv2
从上式可以看出,到达顶点的动能与路径无关
故选B.
本题解析:
本题难度:简单
5、计算题 如图所示,水平桌面上放置一个质量m=1kg的小木块,若用木棒击打木块使木块获得水平方向的初速度v0,木块沿桌面滑出左端边沿,落在水平地面上的D点。已知木块的初速度v0=20m/s,桌面距地面的高度H=3.2m,木块落地的位置距桌面左端边沿的水平距离x=4.8m,忽略空气阻力,取重力加速度g=10m/s2。求:
(1)木块落到地面时的速度大小;
(2)木块离开桌面时的动能;
(3)木块在桌面上滑行过程中克服摩擦力所做的功。
参考答案:(1)10m/s(2)18J(3)182J
本题解析:(1)木块离开桌面后做平抛运动,设运动时间为t,根据自由落体公式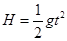 ?
?
木块做平抛运动的时间 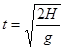 =0.8s?
=0.8s?
木块落地时沿水平方向的分速度? vx=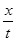 ="6.0" m/s?
="6.0" m/s?
木块落地时沿竖直方向的分速度? vy=gt=8.0 m/s?
木块落到地面时的速度大小?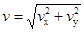 =10.0 m/s?
=10.0 m/s?
(2)根据动能公式,得木块离开桌面时的动能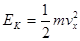 =18 J?
=18 J?
(3)根据动能定理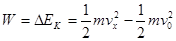 =-182 J?
=-182 J?
故木块在桌面上滑行过程中克服摩擦力所做的功为182 J
本题难度:一般