时间:2017-08-09 08:24:10
1、填空题 汽车通过拱桥顶点时速度为10m/s时，车对桥的压力为车重的
| 3 4 |
参考答案：汽车通过拱桥顶点时速度为10m/s时，受重力，和支持力34mg，
根据牛顿第二定律：mg-34mg=mv2R
代入数据得：R=40m；
如果汽车行驶到桥顶时对桥顶恰无压力，即只受重力，
mg=mv′2R
代入数据得：v′=20m/s
故答案为：40，20．
本题解析：
本题难度：一般
2、选择题 一质量为m的物体，沿半径为R的向下凹的圆形轨道滑行，如图所示，经过最低点的速度为v，物体与轨道之间的动摩檫因数为μ，则它在最低点时受到的摩檫力为（?）
A．μmg
B．μmv2/R
C．μm(g+v2/R)
D．μm(g-v2/R)
参考答案：C
本题解析：在最低点时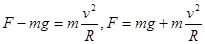
，摩擦力f=μF=μm(g+v2/R)? ,C 对；
本题难度：简单
3、选择题 如图所示，质量为M的物体内有光滑圆形轨道，现有一质量为m的小滑块沿该圆形轨道的竖直面做圆周运动，A、C为圆周的最高点和最低点，B、D与圆心O在同一水平线上．小滑块运动时，物体M保持静止，关于物体M对地面的压力N和地面对物体的摩擦力，下列说法正确的是（ ）
A．滑块运动到A点时，N＞Mg，摩擦力方向向左
B．滑块运动到B点时，N=Mg，摩擦力方向向右
C．滑块运动到C点时，N＞（M+m）g，M与地面无摩擦力
D．滑块运动到D点时，N=（M+m）g，摩擦力方向向左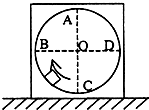
参考答案：A、小滑块在A点时，滑块对M的作用力在竖直方向上，系统在水平方向不受力的作用，所以没有摩擦力的作用，所以A错误．
B、小滑块在B点时，需要的向心力向右，所以M对滑块有向右的支持力的作用，对M受力分析可知，地面要对物体有向右的摩擦力的作用，在竖直方向上，由于没有加速度，物体受力平衡，所以物体M对地面的压力N=Mg，所以B正确．
C、小滑块在C点时，滑块的向心力向上，所以C对物体M的压力要大于C的重力，故M受到的滑块的压力大于mg，那么M对地面的压力就要大于（M+m）g，所以C正确．
D、小滑块在D点和B的受力的类似，由B的分析可知，D错误．
故选BC．
本题解析：
本题难度：简单
4、简答题 如图所示，在同一竖直平面内两正对着的半径为R的相同半圆滑轨道，相隔一定的距离x，虚线沿竖直方向，一质量为m的小球能在其间运动．今在最低点B与最高点A各放一个压力传感器，测试小球对轨道的压力，并通过计算机显示出来．当轨道距离x不同时，测得两点压力差△FN与距离x的图象如右图所示．（不计空气阻力，g取10m/s2
（1）当x=R时，为使小球不脱离轨道运动，求小球在B点的最小速度（用物理量的符号表示）
（2）试写出A、B两点的压力差△FN与?x的函数关系．（用m、R、g表示）
（3）根据图象，求小球的质量和轨道半径．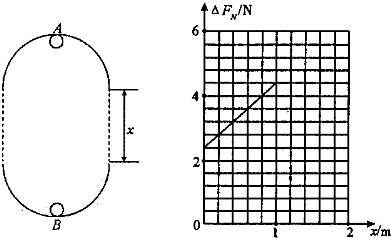
参考答案：
（1）小球恰能在A点沿轨道运动时：
mg=mv2AR?
此时，小球在B点动能最小，由机械能守恒：
12mvB2=mg3R+12mvA2?
解得：vB=
本题解析：
本题难度：一般
5、计算题 如图所示，光滑水平轨道与半径为R的光滑竖直半圆轨道在B点平滑连接．在过圆心O的水平界面MN的下方分布有水平向右的匀强电场．现有一质量为m、电荷量为＋q的小球从水平轨道上A点由静止释放，小球运动到C点离开圆轨道后，经界面MN上的P点进入电场(P点恰好在A点的正上方，如图．小球可视为质点，小球运动到C点之前电荷量保持不变，经过C点后电荷量立即变为零)．已知AB间距离为2R，重力加速度为g.在上述运动过程中，求：
小题1:电场强度E的大小；
小题2:小球在圆轨道上运动时的最大速率；
小题3:小球对圆轨道的最大压力的大小．
参考答案：
小题1:?
小题2: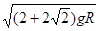
小题3:（2+3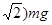
本题解析：分析：（1）对小球从A到C过程运用动能定理列式；小球从C平抛运动到P过程，对水平和竖直分运动分别根据位移公式列式；
（2）小球在圆弧右下段某个位置速度最大，根据动能定理求出速度的一般表达式，然后根据数学知识求最大值；
（3）当速度最大时，小球对轨道的压力最大，根据牛顿第二定律和向心力公式列式求解．
解答：解：（1）设电场强度为E，小球过C点时速度大小为vc，小球从A到C由动能定理：qE?3R-mg?2R=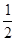
mvc2
小球离开C点后做平抛运动到P点：R=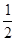gt2，2R=vct
联立方程解得：E=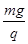
，即电场强度E的大小为．
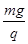（2）设小球运动到圆周D点时速度最大为v，此时OD与竖直线OB夹角设为α，小球从A运动到D过程，根据动能定理：qE(2R+Rsinα)-mgR(1-cosα)= 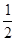mv2
即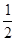：mv2=mgR(sinα+cosα+1)
根据数学知识可得，当α=450时动能最大?
由此可得：vm=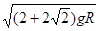
即小球在圆轨道上运动时最大速率为．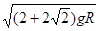
（3）由于小球在D点时速度最大且电场力与重力的合力恰好沿半径方向，故小球在的点对圆轨道的压力最大，设此压力大小为F，由牛顿第三定律可知小球在D点受到的轨道弹力大小也为F，在D点对小球进行受力分析，并建立如图所示坐标系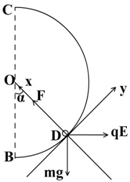
由牛顿第二定律：F-qEsinα-mgcosα=m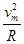
，解得：F=（2+3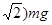
即小球对圆轨道的最大压力的大小（2+3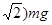
点评：本题关键灵活地选择过程并运用动能定律列式，同时根据向心力公式和平抛运动的位移公式列式进一步分析求解．
本题难度：一般