时间:2017-08-09 08:20:13
1、简答题 已知如图，匀强电场方向水平向右，场强E=1.5×106V/m，丝线长l=40cm，上端系于O点，下端系质量为m=1.0×10-4kg，带电量为q=+4.9×10-10C的小球，将小球从最低点A由静止释放，求：
（1）小球摆到最高点时丝线与竖直方向的夹角多大？
（2）摆动过程中小球的最大速度是多大？（g=9.8m/s2）
参考答案：
（1）在小球运动过程中，重力与电场力是恒定的，则可将此两个力等效成一个力，因此相当于小球受到拉力与等效一个力，类似于“歪摆”，这个“歪摆”．
由于已知电场力Fe=qE=4.9×10-10×1.5×106N=7.35×10-4 N
而重力G=mg=1.0×10-4×9.8N=9.8×10-4 N
因此F：G=3：4，所以摆动到平衡位置时丝线与竖直方向成37°角，因此最大摆角为74°．
（2）小球通过“最低点”即平衡位置时速度最大．在摆过程中拉力不做功，等效的力做正功，
所以由动能定理：
本题解析：
本题难度：一般
2、计算题 如图甲所示，水平加速电场的加速电压为U0，在它的右侧有由水平正对放置的平行金属板a、b构成的偏转电场，已知偏转电场的板长L="0.10" m，板间距离d=5.0×10-2m，两板间接有如图15乙所示的随时间变化的电压U，且a板电势高于b板电势。在金属板右侧存在有界的匀强磁场，磁场的左边界为与金属板右侧重合的竖直平面MN，MN右侧的磁场范围足够大，磁感应强度B=5.0×10-3T，方向与偏转电场正交向里（垂直纸面向里）。质量和电荷量都相同的带正电的粒子从静止开始经过电压U0=50V的加速电场后，连续沿两金属板间的中线OO′方向射入偏转电场中，中线OO′与磁场边界MN垂直。已知带电粒子的比荷
=1.0×108C/kg，不计粒子所受的重力和粒子间的相互作用力，忽略偏转电场两板间电场的边缘效应，在每个粒子通过偏转电场区域的极短时间内，偏转电场可视作恒定不变。
（1）求t=0时刻射入偏转电场的粒子在磁场边界上的入射点和出射点间的距离；
（2）求粒子进入磁场时的最大速度；
（3）对于所有进入磁场中的粒子，如果要增大粒子在磁场边界上的入射点和出射点间的距离，应该采取哪些措施？试从理论上推理说明。
参考答案：
(1)0.40m(2)1.1×105m/s(3)要增大粒子在磁场边界上的入射点和出射点间的距离x，应该减小匀强磁场的磁感应强度B，或增大加速电压U0
本题解析：
（1）设经过加速电场加速后，粒子的速度为v0，根据动能定理有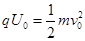
，解得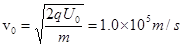
.由于t=0时刻偏转电场的场强为零，所以此时射入偏转电场的粒子将匀速穿过电场而以v0的速度垂直磁场边界进入磁场中，在磁场中的运动轨迹为半圆。
设粒子在磁场中做匀速圆周运动的半径为r，由洛仑兹力公式和牛顿第二定律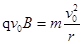得?
解得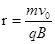 
?所以粒子在磁场边界上的入射点和出射点间的距离d=2r=0.40m
（2）设粒子以最大偏转量离开偏转电场，即轨迹经过金属板右侧边缘处，进入磁场时a、b板的电压为Um，则粒子进入偏转电场后，加速度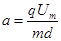
水平方向 L=v0t
竖直方向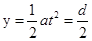 
解得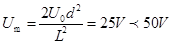
所以，电压Um=25V时对应粒子进入磁场的速度最大，设最大速度大小为vm，方向与OO′的夹角为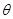
，则对于粒子通过加速电场和偏转电场的过程，根据动能定理有: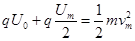
解得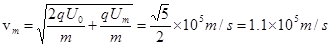 
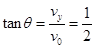，即?
（或
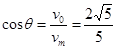，即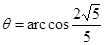
）
（说明：计算结果带有根号，结果正确的同样得分）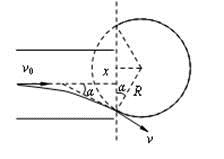
（3）设任意时刻进入磁场的粒子，其进入磁场时速度方向与OO′的夹角为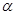
，则其速度大小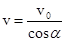
粒子在磁场中做圆周运动的轨迹半径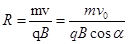
?
由如图所示的几何关系可知，粒子在磁场边界上的入射点和出射点间的距离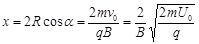
所以要增大粒子在磁场边界上的入射点和出射点间的距离x，应该减小匀强磁场的磁感应强度B，或增大加速电压U0
本题难度：一般
3、简答题 在某次兴趣活动中，设计了如图所示的轨道，AB是光滑的倾斜轨道，底端有一小段将其转接为水平的弧形轨道，BC是一个光滑的水平凹槽，凹槽内放置一个质量为m2=0.5kg的小车，小车上表面与凹槽的两端点BC等高，CDE是光滑的半径为R=6.4cm的竖直半圆形轨道，R是圆轨道的最高点．将一个质量为m1=0.5kg的小滑块，从AB轨道上离B点高h=0.8m处由静止开始释放，滑块下滑后从B点滑上小车，在到达C点之前，滑块与小车达到共同速度，小车与凹槽碰撞后立即停止，此后滑块继续运动，且恰好能经过圆轨道的最高点E，滑块与小车之间的动摩擦因数μ=0.4，g=10m/s2．试求：
（1）小滑块m1经过圆轨道的最高点E时的速度；
（2）小车的长度L和小车获得的最大动能．
参考答案：（1）设m1经过内轨道的最高点E时的速度为vE，
由m1g=m1v2ER
解得：vE=
本题解析：
本题难度：一般
4、选择题 一个高尔夫球静止于平坦的地面上．在i=0时球被击出，飞行中球的速率与时间的关系如图所示．若不计空气阻力的影响，根据图象提供的信息可以求出的量是（ ）
A．高尔夫球在何时落地
B．高尔夫球可上升的最大高度
C．人击球时对高尔夫球做的功
D．高尔夫球落地时离击球点的距离
参考答案：A、不计空气阻力，高尔夫球落到水平地面上时，速率相等．由图看出，小球5s时刻落地．故A正确．
B、小球的初速度大小为v0=31m/s，到达最高点时的速度大小为v=19m/s，由动能定理得-mgh=12mv2-12mv20，由此式可求出最大高度h．故B正确．
C、由动能定理得：人击球时对高尔夫球做的功W=12mv20，由于高尔夫球的质量m未知，无法求出W．故C错误．
D、高尔夫球水平方向做匀速直线运动，水平方向分速度vx=19m/s，高尔夫球落地时离击球点的距离为S=vxt=19×5m=95m．故D正确．
故选ABD
本题解析：
本题难度：简单
5、选择题 一个质量为0.3 kg 的弹性小球，在光滑的水平面上 以6 m/s 的速度垂直撞到墙上，碰撞后小球沿相反的方向运动，反弹后的速度与碰撞前的速度相同，则碰撞前后小球速度变化量的大小△v 和碰撞过程中墙对小球做功的大小W 为
[? ]
A．△v=0
B．△v=12 m/s
C．W=0
D．W=10.8 J
参考答案：BC
本题解析：
本题难度：简单