时间:2017-08-08 08:34:31
1、计算题 如图,ABD为竖直平面内的光滑绝缘轨道,其中AB段是水平的,BD段为半径R=0.2m的半圆,两段轨道相切于B点,整个轨道处在竖直向下的匀强电场中,场强大小E=5.0×103V/m。一不带电的绝缘小球甲,以速度υ0沿水平轨道向右运动,与静止在B点带正电的小球乙发生弹性碰撞。已知乙球的质量为m=1.0×10-2kg,乙所带电荷量q=2.0×10-5C,甲球质量为乙球质量的k倍,g取10m/s2。(水平轨道足够长,甲、乙两球可视为质点,整个运动过程无电荷转移) 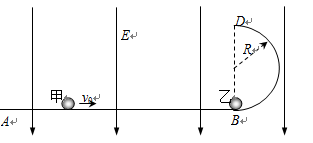
【小题1】若k=1,且甲乙两球碰撞后,乙恰能通过轨道的最高点D,求甲的速度υ0;
【小题2】若k>1,且甲仍以(1)中的速度υ0向右运动,求乙在轨道上的首次落点到B点的距离范围。
参考答案:
【小题1】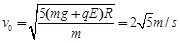
【小题2】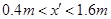
本题解析:(1)在乙恰能通过轨道的最高点的情况下,设乙到达最高点的速度为vD,乙离开D点到达水平轨道的时间为t,乙的落点到B点的距离为x,则ks5u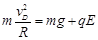 ① (1分)
① (1分)
设碰撞后甲、乙的速度分别为v甲、v乙,根据动量守恒和机械能守恒定律有: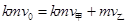 ② (1分)
② (1分)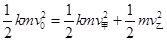 ③ &# www.91exAm.org160; (1分)
③ &# www.91exAm.org160; (1分)
联立②③得: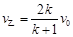 ④ (1分)
④ (1分)
由k=1,则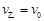
由动能定理得: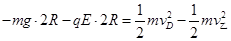 ⑤ (1分)
⑤ (1分)
联立①④⑤得: 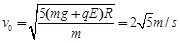 ⑥ (1分)
⑥ (1分)
(2)甲、乙完全弹性碰撞,碰撞后甲、乙的速度分别为v甲、v乙,由②③得
解得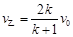 ⑦ (1分)
⑦ (1分)
又k>1,则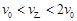 ⑧ (1分)
⑧ (1分)
设乙球过D点的速度为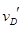 ,由动能定理得
,由动能定理得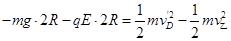 ⑨ (1分)
⑨ (1分)
解得: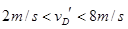 ⑩ (1分)
⑩ (1分)
设乙在水平轨道上的落点到B点的距离为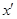 ,则有:
,则有: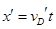 11
11 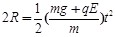 12 (1分)
12 (1分)
联立121314得: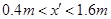 (1分)
(1分)
本题难度:困难
2、计算题 如图所示,A、B两小球分别固定在一刚性轻杆的两端,两球球心间相距L=1m,两球质量分别为mA=4.0kg,m2=1.0kg,杆上距A球球心0.40m处有一水平轴O,杆可绕轴无摩擦转动,现先使杆保持水平,然后从静止释放当杆转到竖直位置,求: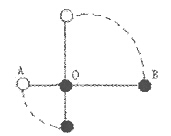
(1)当杆转到竖直位置两球的速度各是多少?
(2)杆对A球的作用力多大;
(3)转动过程中杆对A球做功为多少(计算中重力加速度的数值g=10m/s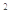 )。
)。
参考答案:(1)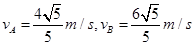 (2)
(2)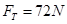 (3)W=-9.6J
(3)W=-9.6J
本题解析:(1)设杆转到竖直位置的角速度为ω,A、B两球的速度分别为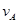 和
和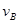
由公式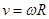 可知
可知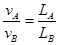
取杆的初位置为零势能面,以两球组成的系统为研究对象,由机械能守恒定律得: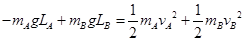
联立得: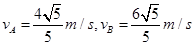
(2)对A用牛顿第二定律: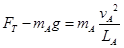 ,解得:
,解得: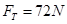
(3)设该过程中杆对A做功为W,对A在该过程用动能定理得: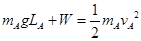 解之得:W=-9.6J
解之得:W=-9.6J
考点:考查了功的计算,圆周运动
本题难度:一般
3、计算题 (18分)如图所示,一滑板B静止在水平面上,上表面所在平面与固定于竖直平面内、半径为R的1/4圆形光滑轨道相切于Q。一物块A从圆形轨道与圆心等高的P点无初速度释放,当物块经过Q点滑上滑板之后即刻受到大小F=2μmg、水平向左的恒力持续作用。已知物块、滑板的质量均为m,滑板与水平面间的动摩擦因数μ,物块与滑板间的动摩擦因数3μ,物块可视为质点,重力加速度取g.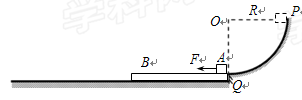
(1)求物块滑到Q点的速度大小;
(2)通过计算判断物块在滑板上滑行过程中,滑板是否滑动;
(3)滑板足够长,求物块A与滑板B之间产生的内能?
参考答案:(1)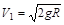 (2)滑板B将向左滑动做加速运动 (3)
(2)滑板B将向左滑动做加速运动 (3)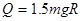
本题解析:(1)物块A从P点运动到Q点的过程中,由动能定理有: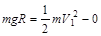 (3分)
(3分)
解得: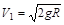 (3分)
(3分)
(2)物块A滑上滑板B时,滑板B在水平方向受到滑块对它的摩擦力f1和水平地面对它的摩擦力f2的作用,其中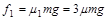 (1分)
(1分)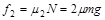 (1分)
(1分)
物块在滑板上滑行的过程中,B受到的合力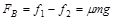 (1分)
(1分)
滑板B将向左滑动做加速运动。(1分)
(3)而F<f1,物块做减速运动,直到两者两速度相等
以物块和滑板组成系统为研究对象,系统水平方向受到的合外力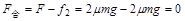 (1分)
(1分)
系统动量守恒定律: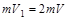 (1分)
(1分)
解得: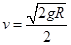 (1分)
(1分)
共速后两者不再分离,一起做匀速运动。
设从B开始运动到A,B恰好同速的过程中,A的位移为L1,B的位移为L2。
对A,由动能定理得: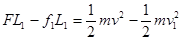 (1分)
(1分)
对B,由动能定理得: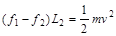 (1分)
(1分)
物块A与滑板B之间产生的内能: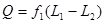 (1分)
(1分)
由以上三式解得: 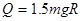 (2分)
(2分)
考点:功能关系 动量守恒定律
本题难度:一般
4、其他 
参考答案: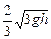
本题解析:以m和M组成的系统为研究对象,系统机械能守恒.则M下降h后速度为v,由机械能守恒定律得:系统减少的重力势能等于增加的动能,则
Mgh=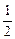 mv2+
mv2+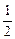 Mv2 ,
Mv2 ,
M=2m,
得v=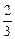
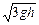
本题难度:简单
5、选择题 如图所示,在固定倾斜光滑杆上套有一个质量为m的圆环,杆与水平方向的夹角α=30°,圆环与竖直放置的轻质弹簧上端相连,弹簧的另一端固定在地面上的A点,弹簧处于原长h。让圆环沿杆由静止滑下,滑到杆的底端时速度恰为零。则在圆环下滑过程中
A.圆环和地球组成的系统机械能守恒
B.当弹簧垂直于光滑杆时圆环的动能最大
C.弹簧的最大弹性势能为mgh
D.弹簧转过60°角时,圆环的动能为
参考答案:CD
本题解析:圆环沿杆滑下,滑到杆的底端的过程中有两个力对圆环做功,即环的重力和弹簧的拉力做功;所以圆环、弹簧和地球组成的系统机械能守恒,由于弹簧的弹性势能发生变化,则圆环与地球组成的系统机械能不守恒,故A错误;从当弹簧垂直于光滑杆到.弹簧转过60°角这个过程中,重力和弹簧的弹力与速度方向的夹角都是锐角,合力是动力,也就是圆环还在做加速运动,所以当弹簧垂直于光滑杆时圆环的动能不是最大,最大动能应该是在弹簧转过角度大于60°的某个位置,大小为 ,故B错误、D正确;当弹簧的最大弹性势能时,重力势能全部转化弹性势能,所以弹簧的最大弹性势能为mgh,故C正确。
,故B错误、D正确;当弹簧的最大弹性势能时,重力势能全部转化弹性势能,所以弹簧的最大弹性势能为mgh,故C正确。
考点:机械能守恒定律
本题难度:一般