时间:2017-08-08 07:52:51
1、选择题 下列说法中错误的是( )
A.磁卡的记录原理是电磁感应现象,读取原理是电流的磁效应
B.日光灯在正常发光时,启动器中的动触片与静触片是分开的
C.电磁炉是利用涡流的热效应来加热物体的
D.电动机、变压器的铁芯用硅钢片代替整块铁芯是为了减小涡流损失
参考答案:A、磁卡以一定的速度通过装有线圈的工作磁头,磁卡的外部磁力线切割线圈,在线圈中产生感应电动势,从而传输了被记录的信号,故A错误;
B、启动器由封在玻璃泡中的静触片和U形动触片组成,玻璃泡中充有氖气.两个触片间加上一定的电压时,氖气导电,发光、发热.动触片是用粘合在一起的双层金属片制成的,受热后两层金属膨胀不同,动触片稍稍伸开一些,和静触片接触. 启动器不再发光,这时双金属片冷却,动触片形状复原,两个触点重新分开,故B正确;
C、电磁炉是通过电子线路板组成部分产生交变磁场、当用含铁质锅具底部放置炉面时,锅具即切割交变磁力线而在锅具底部金属部分产生交变的电流使器具本身自行高速发热,用来加热和烹饪食物,从而达到煮食的目的,故C正确;
D、变压器铁芯会产生涡流,就是铁芯内部产生环状电流,既损失电能,还引起变压器升温造成使用不便和影响性能安全,所以,涡流是越小越好.把整块铁芯改成薄片叠合是减小涡流的方法之一,能有效地减小涡流.整块铁芯的涡流路径最短,所以电阻最小,电流最大.而薄片铁芯的涡流总路径加长,所以电流减小,故D正确;
本题选错误的
故选:A
本题解析:
本题难度:简单
2、选择题 如图所示,图中两条平行虚线间存有匀强磁场,虚线间的距离为2L,磁场方向垂直纸面向里.abcd是位于纸面内的梯形线圈,ad与bc间的距离也为2L且相互垂直,bc边长为2L,t=0时刻,c点与磁场区域左边界重合.现使线圈以恒定的速度v沿垂直于磁场区域边界的方向穿过磁场区域.取沿a→b→c→d→a方向的感应电流为正,则在线圈穿过磁场区域的过程中,感应电流I随时间t变化的关系图线可能是( )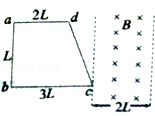
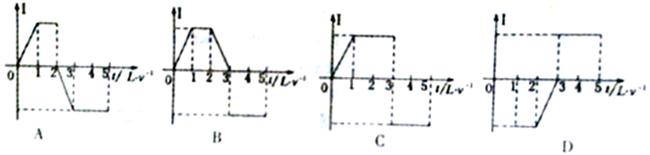
参考答案:B
本题解析:据题意,梯形线框向右运动过程中,cd边在切割磁场,产生的电流方向为逆时针,与正方向一致,在第一个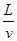 过程中电流大小为:
过程中电流大小为: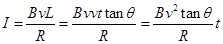 ,选项D错误;当cd边全部进入磁场后,在第二个
,选项D错误;当cd边全部进入磁场后,在第二个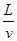 过程中,线框产生的电流为:
过程中,线框产生的电流为: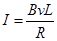 ;当cd边出磁场后,在第三个
;当cd边出磁场后,在第三个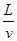 过程中,线框产生的感应电流为:
过程中,线框产生的感应电流为: 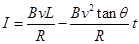 ;在第四个
;在第四个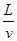 过程中,cd边全部离开磁场,ab边进入,但产生电流顺时针,电流大小为:
过程中,cd边全部离开磁场,ab边进入,但产生电流顺时针,电流大小为: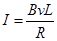 ,故选项B正确而选项AC错误。
,故选项B正确而选项AC错误。
本题难度:一般
3、选择题 下列说法不符合物理学史实的是( ? )
A.库仑通过扭秤实验发现了库仑定律
B.奥斯特最早发现电流周围存在磁场
C.在研究电磁现象时,安培引入了“场”的概念
D.伽利略通过理想实验,说明物体的运动不需要力来维持
参考答案:C
本题解析:
本题难度:简单
4、选择题 下面关于各种电器应用的电磁学原理的说法中,错误的是( ? )
A.电视机的显像管应用了磁场使电子束偏转的原理
B.变压器应用了电磁感应原理
C.微波炉是用电热棒来加热食物的
D.电磁炉也是应用电磁感应原理来工作的
参考答案:C
本题解析:
本题难度:简单
5、填空题 一闭合线圈有50匝,总电阻R=20 Ω,穿过它的磁通量在0.1s内由8×10-3 Wb增加到1.2×10-2 Wb,则线圈中的感应电动势E=?V。
参考答案:2
本题解析:
本题难度:一般