时间:2017-08-08 07:34:51
1、简答题 一匀强磁场,磁场方向垂直于xy平面,在xy平面上,磁场分布在以O为中心的一个圆形区域内.一个质量为m,电荷量为q的带电粒子,由原点O开始运动,初速度为v,方向沿x正方向.后来,粒子经过y轴上的P点,此时速度方向与y轴的夹角为30°,P到O的距离为L,如图所示.不计重力的影响.求磁场的磁感应强度B的大小及xy平面上磁场区域的半径R.
参考答案:粒子在磁场中受到洛伦兹力作用,做匀速圆周运动,则有Bqv=mv2r
?据此并由题意可得,粒子在磁场中的轨迹的圆心C必在y轴上,且P点在磁场区之外.过P沿速度方向作延长线,它与x轴相交于Q点.作圆弧过O点与x轴相切,并且与PQ相切,切点A即粒子离开磁场区的地点.这样也求得圆弧轨迹的圆心C,
如图所示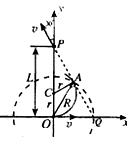
由图中几何关系得:L=3r
由以上两式可得:B=3mvqL
图中OA的长度即圆形磁场区的半径R,由图中几何关系可得
R=
本题解析:
本题难度:一般
2、简答题 在双人花样滑冰比赛中,有时会看到被男运动员拉着的女运动员离开地面在空中做圆锥摆运动的精彩场面,质量为m的女运动员做圆锥摆运动时和水平冰面的夹角为θ,转动过程中女运动员的重心做匀速圆周运动的半径为r,重力加速度为g,求:
(1)该女运动员受到拉力的大小.
(2)该女运动员做圆锥摆运动的周期.
参考答案:以女运动员为研究对象,分析受力情况,受到拉力和重力,
则女运动员受到的拉力
? F=mgsinθ
向心力Fn=mgcotθ,由向心力公式得:
mgcotθ=m4π2rT2
解得:T=
本题解析:
本题难度:一般
3、选择题 光滑的水平轨道AB,与半径为R的光滑的半圆形轨道BCD相切于B点,其中圆轨道在竖直平面内,B为最低点,D为最高点.一质量为m的小球以初速度v0沿AB运动,恰能通过最高点,则( )
A.R越大,v0越大
B.R越大,小球经过B点后的瞬间对轨道的压力越大
C.m越大,v0越大
D.m与R同时增大,初动能Ek0增大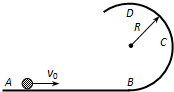
参考答案:
A、C小球恰能通过最高点时,则有mg=v2DR,vD=
本题解析:
本题难度:简单
4、选择题 有两条长短不同、材料相同、同样粗细的绳子,两条绳子各拴着一个质量相同的小球在光滑的水平面上做匀速圆周运动,那么
[? ]
A. 两个球以相同的线速度运动时,长绳易断?
B.两个球以相同的角速度运动时,长绳易断?
C.两个球以相同的周期运动时,短绳易断?
D.不论如何,短绳易断
参考答案:B
本题解析:
本题难度:一般
5、简答题 如图所示,半径R=0.9m的光滑的半圆轨道固定在竖直平面内,直径AC方向竖直向下,下端A与光滑的水平轨道相切.一个质量m=1kg的小球以v0=7m/s的初速度从出发点沿摩擦因数μ=0.2的水平轨道做直线运动,到达A端以vA=3
| 5 |
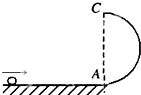
参考答案:(1)在A点,根据向心力公式得:
N-mg=mvA2R
代入数据得:N=60N
根据牛顿第三定律得:小球对轨道的压力为60N
(2)小球恰好能通过最高点C,则在C点只有重力提供向心力,
mg=mvC2R
代入数据解得:vC=3m/s
小球离开C点后,做平抛运动着地,由平抛运动规律可得
2R=12gt2
x=vCt
代入数据解得:x=1.8m
(3)由牛顿第二定律可知:ma=-μmg…①
由运动学公式得:vA2-v02=2aL…②
联立①②两式并代入数据得:L=1m
答:(1)小球刚进入圆周轨道A点时对轨道的压力为60N;
(2)小球从C点离开轨道后的落地点到A点的距离为1.8m;
(3)小球从出发点到A的距离为1m.
本题解析:
本题难度:一般