时间:2017-08-07 16:26:09
1、选择题 关于速度、速度变化量及加速度的说法,正确的是:
A.速度大,加速度不一定大;加速度大,速度一定大
B.速度变化量大,加速度一定大
C.加速度为零,速度可以不为零;速度为零,加速度可以不为零
D.加速度的大小只反映物体速度变化快慢,不能反映物体运动的快慢
参考答案:CD
本题解析:速度大,加速度不一定大,例如高速匀速运动的物体,速度大,但是加速度为零,加速度大,速度也不一定大,A错误,
速度变化量大,加速度不一定大,还要看所用时间,B错误,
加速度的大小只反映物体速度变化快慢,不能反映物体运动的快慢,D正确,
加速度为零,速度可以不为零,如匀速运动;速度为零,加速度可以不为零,如往返运动,C正确,
故选CD
考点:考查了加速度和速度的关系
点评:加速度表示物体速度变化的快慢,由物体所受的合力和物体的质量共同决定,与速度没有直接的关系.
本题难度:一般
2、简答题 汽车速度计是显示汽车瞬时速度的仪表.一辆质量为l000kg的轿车,其行驶过程中,在20s的时间内速度计示数从0增加到72km/h(即20m/s).假定此过程中轿车做匀加速直线运动,受到的阻力恒为500N.求轿车在此过程中所受牵引力的大小.
参考答案:由加速度定义式可知a=v-v0t得:
a=20-020m/s2=1m/s2
由牛顿第二定律得:
? F-f=ma
整理得:F=f+ma
代入数据得:
F=(500+1000×1)N=1500?N?
答:轿车在此过程中所受牵引力的大小为1500N.
本题解析:
本题难度:一般
3、选择题 如图所示,垂直纸面向里的匀强磁场分布在正方形abcd区域内,O点是cd边的中点,一个带正电的粒子仅在磁场力的作用下,从O点沿纸面以垂直于cd边的速度射入正方形内,经过时间t0刚好从c点射出磁场,现设法使该带电粒子从O点沿纸面以与Od成300的方向,以大小不同的速率射入正方形内,那么下列说法中正确的是( )
A.若该带电粒子在磁场中经历的时间是
| 5 3 |
| 2 3 |
| 5 4 |

参考答案:由题,带电粒子以垂直于cd边的速度射入正方形内,经过时间t0刚好从c点射出磁场,则知带电粒子的运动周期为T=2t0.
A、若该带电粒子在磁场中经历的时间是53t?0=56T,粒子轨迹的圆心角为θ=56?2π=53π,速度的偏向角也为53π,根据几何知识得知,粒子射出磁场时与磁场边界的夹角为30°,必定从cd射出磁场.故A正确.
B、当带电粒子的轨迹与ad边相切时,轨迹的圆心角为60°,粒子运动的时间为t=16T=13t0,在所有从ad边射出的粒子中最长时间为13t0,故若该带电粒子在磁场中经历的时间是23t?0,一定不是从ad边射出磁场.故B错误.
C、若该带电粒子在磁场中经历的时间是54t?0=58T,则得到轨迹的圆心角为54π,由于53π>54π>π,则一定从bc边射出磁场.故C正确.
D、若该带电粒子在磁场中经历的时间是t0=12T,则得到轨迹的圆心角为π,而粒子从ab边射出磁场时最大的偏向角等于30°+90°=120°=23π<π,故不一定从ab边射出磁场.故D错误.
故选AC
本题解析:
本题难度:简单
4、简答题 如图(a)所示,在真空中,半径为b的虚线所围的圆形区域内存在匀强磁场,磁场方向与纸面垂直.在磁场右侧有一对平行金属板M和N,两板间距离也为b,板长为2b,两板的中心线O1O2与磁场区域的圆心O在同一直线上,两板左端与O1也在同一直线上.有一电荷量为+q、质量为m的带电粒子,以速率v0从圆周上的P点沿垂直于半径OO1并指向圆心O的方向进入磁场,当从圆周上的O1点飞出磁场时,给M、N板加上如图(b)所示电压u.最后粒子刚好以平行于N板的速度,从N板的边缘飞出.不计平行金属板两端的边缘效应及粒子所受的重力.
(1)求磁场的磁感应强度B;
(2)求交变电压的周期T和电压U0的值;
(3)若t=
| T 2 |
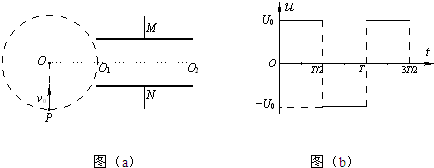
参考答案:
(1)粒子自P点进入磁场向右偏转,从O1点水平飞出磁场,运动的半径必为b,如图一所示:洛伦兹力提供向心力,有: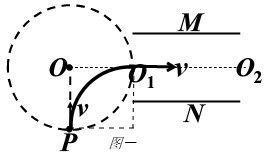
qv0B=mv20b
解得:B=mv0bq
由左手定则可知,磁场方向垂直纸面向外.
(2)粒子自O1点进入电场,做变加速曲线运动,最后恰好从N板的边缘平行飞出(如图二所示),设运动时间为t,则水平方向上有: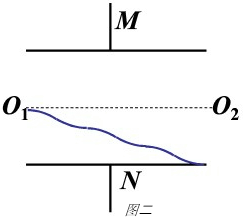
2b=v0t?
在竖直方向上有:
b2=2n?12?qU0mb(T2)2
t=nT(n=1,2,…)?
解得?T=2bnv0(n=1,2,…)?
U0=nmv202q(n=1,2,…)?
(3)当t=T2粒子以速度v0沿O2O1射入电场时,则该粒子恰好从M板边缘以平行于极板的速度射入磁场(如图三所示),且进入磁场的速度仍为v0,运动的轨道半径仍为b.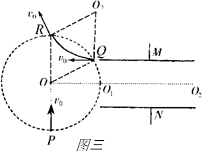
设进入磁场的点为Q,离开磁场的点为R,圆心为O3,如图所示,四边形OQ?O3R是菱形,故O?R∥QO3.?
所以P、O、R三点共线,即POR为圆的直径.即PR间的距离为2b.
答:(1)求磁场的磁感应强度为B=mv0bq,方向垂直纸面向外.
(2)交变电压的周期T为T=2bnv0(n=1,2,…)
电压U0为U0=nmv202q(n=1,2,…),
(3)粒子从磁场中射出的点到P点的距离为2b.
本题解析:
本题难度:一般
5、选择题 一圆盘可绕圆盘中心O且垂直于盘面的竖直轴转动,在圆盘上放置一小木块A,它随圆盘一起运动(做匀速圆周运动),如图所示,则关于木块A的受力,下列说法正确的是
A.木块A受重力、支持力和向心力
B.木块A受重力、支持力和静摩擦力,静摩擦力的方向与木块运动方向相反
C.木块A受重力、支持力和静摩擦力,静摩擦力的方向指向圆心
D.木块A受重力、支持力和静摩擦力,静摩擦力的方向与木块运动方向相同
参考答案:C
本题解析:试题分析:对木块受力分析可知,木块受到重力、支持力和摩擦力的作用,重力是竖直向下的,支持力是竖直向上的,重力和支持力都在竖直方向上,这两个力为平衡力,只有摩擦力作为了物体做圆周运动的向心力,所以摩擦力的方向应该是指向圆心的,故选C
考点:考查了向心力
点评:圆周运动都需要向心力,向心力是由其他的力来充当的,向心力不是一个单独力.
本题难度:一般