时间:2017-08-07 16:18:59
1、选择题 在一个匀强电场中有a、b两点，相距为d，电场强度为E，把一个电量为q的负电荷由a移到b点时，电场力对电荷做正功W，以下说法正确的是（?）
A．a点电势比b点电势低
B．a、b两点电势差大小为U=Ed
C．a、b两点电势差大小为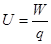
D．该电荷在b 点电势能较在a点大
参考答案：AC
本题解析：根据把一个电量为q的负电荷由a移到b点时，电场力对电荷做正功，可知电场力由a指向b，所以场强方向由b指向a，沿着电场线方向电势降低，a点电势较低，A对；电场力做正功电势能减小，D错；由匀强电场U=Ed，d为AB两点沿着电场线方向的投影，不一定是两点间的距离，B错；公式W=qU适用于任何电场，D对
点评：本题难度较小，要知道电场线与场强、电势间的关系，只要电场力做正功电势能肯定减小
本题难度：简单
2、简答题 右图中A和B表示在真空中相距为d的两平行金属板加上电压后，它们之间的电场可视为匀强电场；右边表示一周期性的交变电压的波形，横坐标代表时间t，纵坐标代表电压UAB，从t=0开始，电压为给定值U0，经过半个周期，突然变为-U0……。如此周期地交替变化。在t=0时刻将上述交变电压UAB加在A、B两极上，求：
(1)?在t=0时刻，在B的小孔处无初速地释放一电子，在t=3T/4时电子的速度大小？（一个周期内电子不会打到板上，T作为已知）
(2) 在t=?时刻释放上述电子，在一个周期时间，该电子刚好回到出发点?试说明理由并具备什么条件。?
(3)在t=0时刻，在B的小孔处无初速地释放一电子，要想使这电子到达A板时的速度最小(零)，则所加交变电压的周期为多大?
（4）在t=0时刻，在B的小孔处无初速地释放一电子，要想使这电子到达A板时的速度最大，则所加交变电压的周期最小为多少?
参考答案：(1)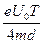 
?(2) 
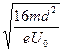?(3) T＝
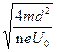(n＝1，2，3，…) (4) 
本题解析：电子在两极板间运动的V-t图象如右图所示。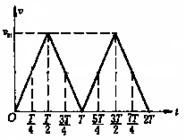
(1) 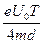（4分）
(2)在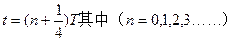
时刻释放电子，经过一个周期，电子刚回到出发点。条件是在半个周期即从(
～
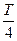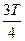)时间内，电子的位移小于d，亦即频率T≤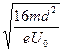。（6分）
(3)由电子在电场中运动时的受力情况及速度变化情况可知：要求电子到达A板的速度为零，则电子应该在t＝nT(n＝1，2，3，…)时刻到达A板，电子在每个
内通过的位移为：
S＝
×
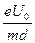×（）2?③
依题意知：d＝n(2S)?
综合③、可得：T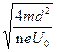＝(n＝1，2，3，…)。（6分）
(4)要求电子到达A板的速度最大，则电子应该从B板一直加速运动到A板，即电子从B板加速运动到A板所用时间必须满足：t≤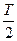
①?
依题意知：S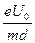＝××t2＝d ②
综合①、②可得：Tmin=。（6分
本题难度：一般
3、简答题 两平行金属板竖直放置，距离为d．把它们分别与电压为U的直流电源两极相连，如图所示．一个质量为m、电荷量为q的带电微粒位于两金属板上端的中点处，无初速释放，最后落在某一金属板上，微粒到达该金属板时的动能为Ek．现保持其他条件不变，使电压U加倍，问满足怎样的条件，微粒到达该金属板时的动能仍为Ek？
参考答案：
本题解析：
设微粒带的是正电荷，它将落到右边的金属板上．它在电场中运动的过程中，电场力做功W1=qU/2．
它在水平方向上的分运动是初速为零的匀加速运动，运动时间为t，
则
，
．
它在竖直方向的分运动是自由落体运动，竖直分位移
，
运动过程中电场力做功W2=mgh=
．
根据动能定理，微粒到达金属板时的动能Ek=W1+W2=
．
现要求U加倍而Ek不变，即
=，
解出应满足的条件是．
本题难度：一般
4、计算题 如图，在x轴上方存在匀强磁场，磁感应强度大小为B，方向垂直于纸面向外；在x轴下方存在匀强电场，场强大小为E，电场方向与xoy平面平行，且与x轴成450夹角。一质量为m、电荷量为q（q＞0）的粒子以速度v0从y轴上P点沿y轴正方向射出，一段时间后进入电场，进入电场时的速度方向与电场方向相反；从粒子进入电场开始经过某一段时间T0（T0未知），磁场方向变为垂直纸面向里，大小不变，结果能使粒子返回到P点（不计粒子重力）
（1）粒子磁场中运动半径R
（2）粒子第一次经过x轴时的坐标位置
（3）从P点出发到再次回到P点的时间
参考答案：(1)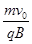
(2) 
(3)
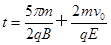
本题解析：（1）根据牛顿定律可知，粒子在磁场中运动的向心力由洛伦兹力提供，则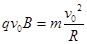
，解得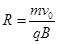
；
（2）由粒子的运动轨迹及几何关系可知，粒子第一次经过x轴时的坐标位置为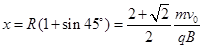
（3）粒子在磁场中先做匀速圆周运动，然后进入电场中作匀减速运动，然后反向做匀加速运动，回到磁场中继续做匀速圆周运动回到P点，则在磁场中运动的时间：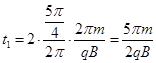
粒子在电场中的加速度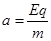
，在电场中运动的总时间：
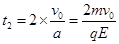，故粒子从P点出发到再次回到P点的时间为：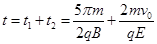
考点：带电粒子在匀强电场及在匀强磁场中的运动.
本题难度：一般
5、其他 
参考答案：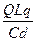
本题解析：从功的公式角度出发考虑沿不同方向移动杆与球，无法得出电场力所做功的数值。但从电场力对两个小球做功引起两小球电势能的变化这一角度出发，可以间接求得电场力对两个小球做的总功。只要抓住运动的起点、终点两个位置两小球的电势能之和就能求出电场力的功。
初始两小球在很远处时各自具有的电势能为零，所以E0=0；终点位置两球处于图11所示的静止状态时，设带正电小球的位置为a，该点的电势为Ua，则带正电小球电势能为qUa;设带负电小球的位置为b，该点的电势为Ub，则带负电小球电势能为-qUb.所以两小球的电势能之和为：
Et=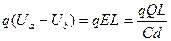
所以电场力对两小球所做的功为：
，即两个小球克服电场力所做总
功的大小等于。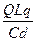
本题难度：一般