时间:2017-08-07 16:18:59
1、计算题 如图所示,K与虚线MN之间是加速电场,虚线MN与PQ之间是匀强电场,虚线PQ与荧光屏之间是匀强磁场,且MN、PQ与荧光屏三者互相平行,电场和磁场的方向如图所示,图中A点与O点的连线垂直于荧光屏.一带正电的粒子从A点离开加速电场,速度方向垂直于偏转电场方向射入偏转电场,在离开偏转电场后进入匀强磁场,最后恰好垂直地打在荧光屏上.已知电场和磁场区域在竖直方向足够长,加速电场电压与偏转电场的场强关系为U= Ed,式中的d是偏转电场的宽度,磁场的磁感应强度B与偏转电场的电场强度E和带电粒子离开加速电场的速度v0关系符合表达式v0=
Ed,式中的d是偏转电场的宽度,磁场的磁感应强度B与偏转电场的电场强度E和带电粒子离开加速电场的速度v0关系符合表达式v0=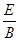 .若题中只有偏转电场的宽度d为已知量。
.若题中只有偏转电场的宽度d为已知量。
(1)画出带电粒子轨迹示意图。
(2)磁场的宽度L为多少?
(3)带电粒子在电场和磁场中垂直于v0方?向的偏转距离分别是多少?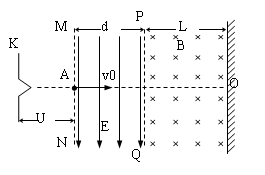
参考答案:(1)轨迹如图所示;(2)L= d;(3)0.914d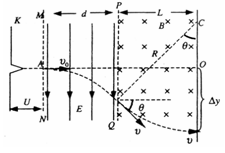
本题解析:
试题分析: (1)轨迹如图所示。?
(2)粒子在加速电场中,由动能定理有?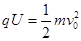
粒子在匀强电场中做类平抛运动,设偏转角为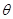 ,有
,有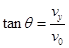 ?
?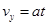 ?
?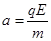 ?
?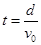 ?U=
?U= Ed?
Ed?
解得:θ=45?
由几何关系得,带电粒子离开偏转电场速度为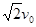
粒子在磁场中运动,由牛顿第二定律有:qvB=m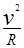
在磁场中偏转的半径为 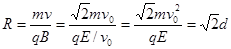
由图可知,磁场宽度L=Rsinθ="d"
(3)由几何关系可得:
带电粒子在偏转电场中距离为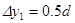 ,
,
在磁场中偏转距离为
粒子在电场、磁场中偏转的总距离为△y=△y1+△y2=0.914d
本题难度:一般
2、选择题 示波管可以视为加速电场和偏转电场的组合.若已知前者的电压为U1,而后者电压为U2,极板长为L,板间距为d.电子加速前速度可忽略,则示波管的灵敏度(偏转电场中每单位偏转电压所引起的偏转量称为“灵敏度”?)与加速电场和偏转电场关系正确的是?
[? ]
A.L越大,灵敏度越大 ?
B.d越大,灵敏度越大 ?
C.U1越小,灵敏度越大 ?
D.灵敏度与U1无关
参考答案:AC
本题解析:
本题难度:一般
3、选择题 如图所示,电子在电压为U1的电场中由静止加速后,垂直射入电压为U2的偏转电场. 在满足电子能射出偏转电场的条件下,下列四种情况中,一定能使电子的偏转角变大的是(?)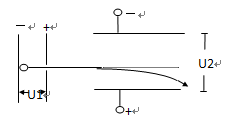
A.U1变大, U2变大
B.U1变小, U2变大
C.U1变大, U2变小
D.U1变小, U2变小
参考答案:B
本题解析:由动能定理,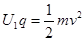 -0?
-0?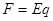 ,
,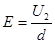 ,
,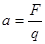 ?
?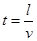
tanθ= =
=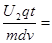
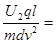
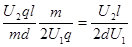
所以,要想使偏角变大,可以U1变小, U2变大。选B选项。
本题难度:简单
4、计算题 (12分)如图所示,在 轴上方有一竖直向下的匀强电场区域,电场强度为
轴上方有一竖直向下的匀强电场区域,电场强度为 。
。 轴下方分布有很多磁感应强度为
轴下方分布有很多磁感应强度为 的条形匀强磁场区域,其宽度均为为
的条形匀强磁场区域,其宽度均为为 ,相邻两磁场区域的间距为
,相邻两磁场区域的间距为 。现将一质量为
。现将一质量为 、电荷量为
、电荷量为 的带正电的粒子(不计重力)从
的带正电的粒子(不计重力)从 轴上的某处静止释放。
轴上的某处静止释放。
(1)若粒子从坐标(0, )点由静止释放,要使它经过
)点由静止释放,要使它经过 轴下方时,不会进入第二磁场区,
轴下方时,不会进入第二磁场区, 应满足什么条件?
应满足什么条件?
(2)若粒子从坐标(0, )点由静止释放,求自释放到第二次过
)点由静止释放,求自释放到第二次过 轴的时间。
轴的时间。
参考答案:(1) (2)
(2)
本题解析:(1)粒子经电场加速,经过 轴时速度大小为
轴时速度大小为 ,满足:
,满足: ?
?
之后进入下方磁场区,依据题意可知运动半径应满足: ?
?
又 ?
?
由以上三式可得: ?
?
(2)当粒子从 的位置无初速释放后,先在电场中加速,加速时间为
的位置无初速释放后,先在电场中加速,加速时间为 满足
满足
解得 ?
?
进入磁场的速度大小为 ,圆周运动半径为
,圆周运动半径为

解得
 ?
?
 ?
?
解得: ?
?
根据粒子在空间运动轨迹可知,它最低能进入第二个磁场区,它在磁场区共运动时间为半个圆周运动的时间 ,经过第一无磁场区时运动方向与
,经过第一无磁场区时运动方向与 轴的夹角
轴的夹角 满足:
满足: ?
?
所以它在无磁场区的路程 ?
?
无磁场区运动时间 ?
?
总时间 ?
?
点评:该题是一道综合性较强的题,主要是考察了带电粒子在电场中的加速、偏转和在磁场的匀速圆周运动.解决此类问题常用的方法是对过程进行分段,对各个段内的运动情况进行具体分析,利用相关的知识进行解答.这要求我们要对带电粒子在电场和磁场中的运动规律要了如指掌,尤其是带电粒子在磁场中的偏转,确定轨迹的圆心是解决此类问题的关键.
本题难度:一般
5、计算题 如图所示,abcd是一个正方形盒子.cd边的中点有一个小孔e.盒子中有沿ad方向的匀强电场,一个质量为m带电粒子从a处的小孔沿ab方向以初速度v0射入盒内,并恰好从e处的小孔射出。求: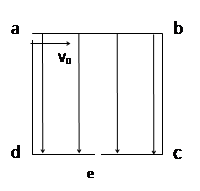
⑴该带电粒子从e孔射出时的速度大小。
⑵该过程中电场力对该带电粒子做的功。
参考答案:⑴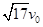 ?(2)
?(2)
本题解析:⑴把ve正交分解,其水平分速度为v0和竖直分速度为vy。
水平匀速直线运动: ?(1)
?(1)
竖直初速为零的匀加速: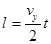 ?(2)
?(2)
由(1)(2)得: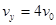 ?
?
所以有:ve=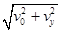 =
=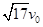 ?(3)
?(3)
⑵a到e过程,根据动能定理得:
W电=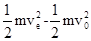 =
=
点评:本题考察了带电粒子在电场中的类平抛运动知识,通过平抛的处理方法处理类平抛。
本题难度:一般