时间:2017-08-07 15:54:37
1、计算题 (8分)如图所示,水平地面上有一个坑,其竖直截面为半圆,O为圆心,且B为沿水平方向的直径。若在A点以初速度v1沿AB方向平抛一小球,小球将击中坑壁上的最低点D;而在C点以初速度v2沿BA方向平抛的小球也能击中D点。已知∠COD=600,求两小球初速度之比v1:v2。(小球视为质点)
参考答案:
本题解析:本题为平抛运动问题,也属于容易题。
小球从A点平抛,可得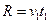 ? 1分?
? 1分?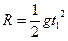 ?1分
?1分
小球从C点平抛,可得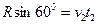 ? 1分?
? 1分?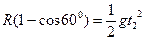 ? 1分
? 1分
联立解得 ? 4分
? 4分
本题难度:一般
2、简答题 如图,一质量为M的物块静止在桌面边缘,桌面离水平地面的高度为h.一质 91Exam.org量为m的子弹以水平速度v0射入物块后,以水平速度v0/2?射出.重力加速度为g.求:
(1)子弹穿出木块时木块的速度大小;
(2)此过程中系统损失的机械能;
(3)此后物块落地点离桌面边缘的水平距离.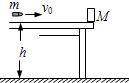
参考答案:(1)设子弹穿过物块后物块的速度为V,由动量守恒得mv0=m?v02+MV? ①
? 解得V=m2Mv0? ?②
? (2)系统的机械能损失为 △E=12mv20-[12m(v02)2+12MV2]?③
? 由②③式得△E=18(3-mM)mv20④
? (3)设物块下落到地面所需时间为t,落地点距桌边缘的水平距离为s,
? 则h=12gt2? ⑤
? s=Vt?⑥
? 由②⑤⑥式得 s=mv0M
本题解析:
本题难度:一般
3、选择题 甲、乙两人从距地面h高处同一位置抛出两个小球,甲球的落地点距抛出点的水平距离是乙球的2倍,不计空气阻力,为了使乙球的落地点与甲球相同,则乙抛出点的高度应为
[? ]
A.4h
B.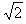 h
h
C.2h
D.3h
参考答案:A
本题解析:
本题难度:简单
4、填空题 如图,子弹从O点水平射出,初速度为v0,穿过两块竖直放置的薄挡板A和B,留下弹孔C和D,测量C和D的高度差为0.1 m,两板间距4 m,A板离O点的水平距离为14 m,不计挡板和空气的阻力,则v0="________" m/s (g=10 m/s2)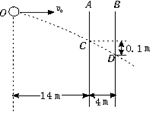
参考答案:80
本题解析:假设子弹穿过A板的时间为t1,穿过B板的时间为t2,根据平抛运动的规律有:
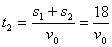 穿过两板的高度差:
穿过两板的高度差:
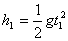
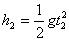 联立以上各式解得:v0=80m/s
联立以上各式解得:v0=80m/s
本题难度:简单
5、填空题 在做研究平抛运动的实验时,让小球多次沿同一轨道运动,通过描点法画出小球平抛运动的轨迹.为了能较准确地描绘运动轨迹,以下操作要求正确的是______
A.通过调节使斜槽的末端切线水平
B.每次释放小球的位置必须不同
C.每次必须由静止释放小球
D.小球运动时不应与木板上的白纸(或方格纸)相碰.
参考答案:A、通过调节使斜槽末端保持水平,是为了保证小球做平抛运动.故A正确.
B、C因为要画出小球同一运动的轨迹,必须每次释放小球的位置相同,且由静止释放,以保证获得相同的初速度.故B错误,C正确.
D、实验要求小球滚下时不能碰到木板平面,避免因摩擦而使运动轨迹改变.故D正确.
故选ACD.
本题解析:
本题难度:简单