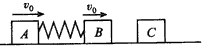时间:2017-08-07 15:37:01
1、计算题 用放射源钋的α射线轰击铍时，能发射出一种穿透力极强的中性射线，这就是所谓铍“辐射”。1932年，查德威克用铍“辐射”分别照射（轰击）氢和氨（它们可视为处于静止状态）。测得照射后沿铍“辐射”方向高速运动的氨核和氦核的质量之比为7.0。查德威克假设铍“辐射”是由一种质量不为零的中性粒子构成的，从而通过上述实验在历史上首次发现了中子。假设铍“辐射”中的中性粒子与氢或氦发生弹性正碰，试在不考虑相对论效应的条件下计算构成铍“辐射”的中性粒子的质量。（质量用原子质量单位u表示，1 u等于1个12C原子质量的十二分之一。取氢核和氦核的质量分别为1.0 u和14 u。）
参考答案：解：设构成铍“辐射”的中性粒子的质量和速度分别为m和v，氢核的质量为mH。构成铍“辐射”的中性粒子与氢核发生弹性正碰，碰后两粒子的速度分别为v"和vH"
由动量守恒与能量守恒定律得：mv＝mv′＋mHvH′ 
解得：
同理，对于质量为mN的氮核，其碰后速度为
可求得：
根据题意可知：vH′＝7.0vN′
解得：m＝1.2u
本题解析：
本题难度：困难
2、计算题 （选修3-5选做题）
如图所示，物体A、B的质量分别是mA=4kg、mB=6kg，用轻弹簧相连接放在光滑的水平面上，物体B左侧与竖直墙相接触。另有一个物体C以速度v0=6m/s向左运动，与物体A相碰，碰后立即与A粘在一起不再分开，然后以v=2m/s的共同速度压缩弹簧，试求：
（1）物块C的质量mC；
（2）在B离开墙壁之后，弹簧的最大弹性势能。
参考答案：解：（1）对A、C在碰撞过程中动量守恒
可知：
代入可得：
=2kg
（2）当B离开墙壁时，弹簧处于原长，A、C以2m/s速度向右运动。当A、B、C获得共同速度时，弹簧弹性势能最大
对A、B、C系统，动量守恒可知：
可得：
由能量守恒可知：
本题解析：
本题难度：一般
3、计算题 在水平桌面上沿一条直线放两个完全相同的小物块A和B（可看作质点）质量均为m，它们相距s。B到桌边的距离是2s。对A施以瞬间水平冲量I，使A沿A、B连线以速度v0向B运动。设两物体碰撞时间很短，碰后不再分离。为使两物体能发生碰撞，且碰撞后又不会离开桌面，求：
（1）物体A、B与水平面间的动摩擦因数μ应满足什么条件；
（2）若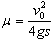
，那么A、B碰撞过程系统损失的动能是多少？A、B停止运动时，到桌面右边缘的距离s′是多少？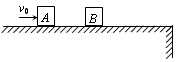 
参考答案：（1）
≤μ＜
（2）mv02/8，7s/4
本题解析：
本题难度：困难
4、计算题 （9分）如图所示，在光滑水平地面上，有一右端装有固定的竖直挡板的平板小车质量
m1＝4.0kg，挡板上固定一轻质细弹簧．位于小车上A点处的质量为m2＝1.0 kg的木块(视为质点)与弹簧的左端相接触但不连接，此时弹簧与木块间无相互作用力。木块与车面之间的摩擦可忽略不计。现小车与木块一起以v0＝2.0 m/s的初速度向右运动，小车将与其右侧的竖直墙壁发生碰撞，已知碰撞时间极短，碰撞后小车以v1＝1.0 m/s的速度水平向左运动，取g＝10 m/s2。求：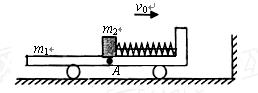
(i)小车与竖直墙壁发生碰撞的过程中小车动量变化量的大小；
(ii)若弹簧始终处于弹性限度内，求小车撞墙后与木块相对静止时的速度大小和弹簧的最大弹性势能。
参考答案：（1）
?（2）
本题解析：（ⅰ）以v1的方向为正方向，则小车与竖直墙壁发生碰撞的过程中，小车动量变化量的大小为?
?①? 2分
（ⅱ）小车与墙壁碰撞后向左运动，木块与小车间发生相对运动将弹簧压缩至最短时，二者速度大小相等，此后木块和小车在弹簧弹力的作用下，做变速运动，当两者具有相同速度时，二者相对静止。整个过程中，小车和木块组成的系统动量守恒
设小车和木块相对静止时的速度大小为v，根据动量守恒定律有
? ② 2分
解得?
?③ 1分
当小车与木块首次达到共同速度
时，弹簧压缩至最短，此时弹簧的弹性势能最大
设最大弹性势能为EP，根据机械能守恒定律可得 
?④ 2分 ?⑤ 2分
本题难度：困难
5、计算题 光滑水平面上，用弹簧相连接的质量均为2 kg的A、B两物体都以v0=6 m/s速度向右运动，弹簧处于原长。质量为4 kg的物体C静止在前方，如图所示，B与C发生碰撞后粘合在一起运动，在以后的运动中，求：
（1）弹性势能最大值为多少？
（2）当A的速度为零时，弹簧的弹性势能为多少？ 
参考答案：解：（1）B、C碰撞瞬间，B、C的总动量守恒，由动量守恒定律得：
mBv0=(mB+mC)v
v=2 m/s
三个物体速度相同时弹性势能最大，由动量守恒定律得：
mAv0+mBv0= (mA+mB+mC)v共
v共=3m/s
设最大弹性势能为Ep，由能量守恒得：
12 J
（2）当A的速度为零时，由动量定恒定律得：
mAv0+mBv0=(mB+mC)vBC
vBC=4 m/s
则此时的弹性势能
本题解析：
本题难度：困难