时间:2017-08-05 17:37:43
1、简答题 如图所示,长为L的细绳上端系一质量不计的环,环套在光滑水平杆上,在细线的下端吊一个质量为m的铁球(可视作质点),球离地的高度h=L,当绳受到大小为3mg的拉力时就会断裂。现让环与球一起以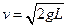 的速度向右运动,在A处环被挡住而立即停止,A离右墙的水平距离也为L。不计空气阻力,已知当地的重力加速度为g。试求:
的速度向右运动,在A处环被挡住而立即停止,A离右墙的水平距离也为L。不计空气阻力,已知当地的重力加速度为g。试求:
(1)在环被挡住而立即停止时绳对小球的拉力大小;
(2)在以后的运动过程中,球的第一次碰撞点离墙角B点的距离是多少?
参考答案:绳对小球的拉力大小为F=3mg
球的第一次碰撞点距B的距离为
本题解析:(1)在环被挡住而立即停止后小球立即以速率v绕A点做圆周运动,根据牛顿第二定律和圆周运动的向心力公式有
解得绳对小球的拉力大小为F=3mg
(2)根据上面的计算可知,在环被A挡住的瞬间绳恰好断裂,此后小球做平抛运动.
假设小球直接落到地面上,则
球的水平位移
所以小球先与右边的墙壁碰撞后再落到地面上
设球平抛运动到右墙的时间为 ,则
,则
小球下落的高度
所以球的第一次碰撞点距B的距离为 。
。
本题难度:一般
2、选择题 如图所示是一个内壁光滑的锥形漏斗,其轴线垂直于水平面,锥形漏斗固定不动,两个质量相同的球A、B紧贴着漏斗内壁分别在图中所示的水平面内做匀速圆周运动,则
A.球A的线速度必小于球B的线速度
B.球A的加速度必小于球B的加速度
C.球A的角速度必小于球B的角速度
D.球A所受合力必大于球B所受合力
参考答案:C
本题解析:两小球受重力和支持力,靠重力和支持力的合力提供做圆周运动的向心力,两小球所受的重力大小相等,支持力方向相同,根据力的合成知识,知两支持力大小相等,两球受到的合力大小相等.根据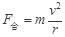 ,得,v=
,得,v=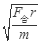 ,合力、质量相等,r大则线速度大,所以球A的线速度大于球B的线速度.根据
,合力、质量相等,r大则线速度大,所以球A的线速度大于球B的线速度.根据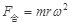 ,得ω=
,得ω=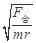 ,r大则角速度小,所以球A的角速度小于球B的角速度.根据
,r大则角速度小,所以球A的角速度小于球B的角速度.根据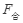 =ma,知向心加速度相等.综上可知,本题选C。
=ma,知向心加速度相等.综上可知,本题选C。
本题难度:一般
3、选择题 如图,一细绳的上端固定在天花板上靠近墙壁的O点,下端拴一小球.L点是小球下垂时的平衡位置.Q点代表一固定在墙上的细长钉子,位于OL直线上.N点在Q点正上方,且QN=QL.M点与Q点等高.现将小球从竖直位置(保持绳绷直)拉开到与N等高的P点,释放后任其向L摆动.运动过程中空气阻力可忽略不计.小球到达L后,因细绳被长钉挡住,将开始沿以Q为中心的圆弧继续运动.在这以后( )?
A.小球向右摆到M点,然后就摆回来
B.小球向右摆到M和N之间圆弧上某点处,然后竖直下落
C.小球沿圆弧摆到N点,然后竖直下落
D.以上说法都不对
参考答案:C
本题解析:小球向右摆一定可以超过跟O点等高的M点,故A错误
小球做圆周运动一定具有向心力,假设可以到N点根据机械能守恒定律可知速度为零,但是到最高点的最小速度是重力提供向心力,即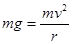 ,可知速度不可以为零,则不能摆到N点,故C错误
,可知速度不可以为零,则不能摆到N点,故C错误
小球做圆周运动超过M点未到N点之前,绳子上无拉力时速度最小,因为重力始终存在指向圆心的分力,所以速度始终不为零,始终存在竖直速度,那么也就不可能竖直下落,故B错误
没有正确结论所以应该选D
本题难度:简单
4、填空题 一辆质量为4t的汽车驶过半径为50m的凸形桥面时,始终保持5m/s的速率,汽车所受阻力为车与桥面间压力的0.05倍(g取10m/s2),求通过最高点时汽车对桥面的压力为?,此时汽车的牵引力大小为?
参考答案:38000? 1900
本题解析:本题考查的是拱桥问题,由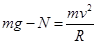 ,通过最高点时汽车对桥面的压力
,通过最高点时汽车对桥面的压力 ;此时汽车的牵引力大小与阻力大小相等
;此时汽车的牵引力大小与阻力大小相等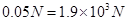 ;
;
本题难度:一般
5、填空题 甲、乙两颗人造地球卫星围绕地球做匀速圆周运动,它们的质量之比
m1:m2=1:2,它们做圆周运动的轨道半径之比为r1:r2=1:2,则它们的向心力之比F1:F2=_______,角速度之比 :
: =_______.
=_______.
参考答案:2:1,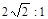
本题解析:由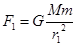 ,
,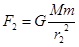 得
得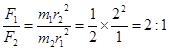 ;由
;由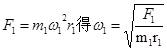 ,同理得
,同理得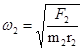 ,则
,则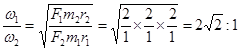
本题难度:简单