时间:2017-08-05 17:28:03
1、选择题 在匀强磁场中，a、b是两条平行金属导轨，而c、d为串有电流表、电压表的两金属棒，如图所示，两棒以相同的速度向右匀速运动，则以下结论正确的是（ ）
A．电压表有读数，电流表没有读数
B．电压表有读数，电流表也有读数
C．电压表无读数，电流表有读数
D．电压表无读数，电流表也无读数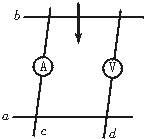
参考答案：D
本题解析：
本题难度：简单
2、简答题 如图所示，两根间距为L的金属导轨MN和PQ，电阻不计，左端弯曲部分光滑，水平部分导轨与导体棒间的滑动摩擦因数为μ，水平导轨左端有宽度为d、方向竖直向上的匀强磁场Ⅰ，右端有另一磁场Ⅱ，其宽度也为d，但方向竖直向下，两磁场的磁感强度大小均为B0，相隔的距离也为d．有两根质量为m、电阻均为R的金属棒a和b与导轨垂直放置，b棒置于磁场Ⅱ中点C、D处．现将a棒从弯曲导轨上某一高处由静止释放并沿导轨运动下去．
（1）当a棒在磁场Ⅰ中运动时，若要使b棒在导轨上保持静止，则a棒刚释放时的高度应小于某一值h0，求h0的大小；
（2）若将a棒从弯曲导轨上高度为h（h＜h0）处由静止释放，a棒恰好能运动到磁场Ⅱ的左边界处停止，求a棒克服安培力所做的功；
（3）若将a棒仍从弯曲导轨上高度为h（h＜h0）处由静止释放，为使a棒通过磁场Ⅰ时恰好无感应电流，可让磁场Ⅱ的磁感应强度随时间而变化，将a棒刚进入磁场Ⅰ的时刻记为t=0，此时磁场Ⅱ的磁感应强度为B0，试求出在a棒通过磁场Ⅰ的这段时间里，磁场Ⅱ的磁感应强度随时间变化的关系式．
参考答案：（1）因为a棒进入磁场Ⅰ后做减速运动，所以只要刚进入时b棒不动，b就可以静止不动．对a棒：由机械能守恒：mgh0=12m02，
对回路：ε=BLv0，I=ε2R
对b棒：BIL=μmg
联立解得：h0=2μ2m2gR2B4L4
（2）由全过程能量守恒与转化规律：mgh=μmg2d+W克A
解得：W克A=mgh-μmg2d
（3）a棒通过磁场Ⅰ时恰好无感应电流，说明感应电动势为零，根据法拉第电磁感应定律ε=△Φ△t，在△t≠0的前提下，△Φ=0即Φ保持不变
对a棒：由机械能守恒：mgh=12mv2
a棒进入磁场Ⅰ后，由牛顿第二定律得：a=μg
经过时间t，a棒进入磁场Ⅰ的距离为x=vt-12at2
磁通量Φ=B0（d-x）L-Bd2L
又最初磁通量为Φ0=B0dL-B0d2L=12B0dL=Φ
联立解得：B=B0-2B0d(
本题解析：
本题难度：一般
3、选择题 如图所示，足够长的U型光滑金属导轨平面与水平面成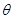
角（0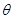＜＜90°),其中MN平行且间距为L，导轨平面与磁感应强度为B的匀强磁场垂直，导轨电阻不计。金属棒
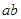由静止开始沿导轨下滑，并与两导轨始终保持垂直且良好接触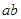，棒的电阻为R，当流过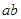棒某一横截面的电量为q时，它的速度大小为
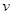，则金属棒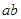在这一过程中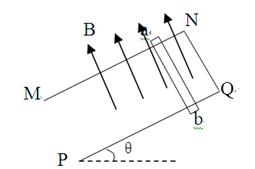
A．运动的平均速度大小为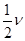
B．平滑位移大小为
C．产生的焦耳热为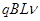
D．受到的最大安培力大小为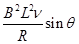
参考答案：B
本题解析：A、金属棒ab开始做加速度逐渐减小的变加速运动，不是匀变速直线运动，平均速度不等于
，而是大于；错误
B、由电量计算公式
可得，下滑的位移大小为
；正确
C、产生的焦耳热
，而这里的电流I比棒的速度大小为v时的电流
小，故这一过程产生的焦耳热小于
；错误
D、金属棒ab受到的最大安培力大小为
；错误
故选B
点评：电磁感应综合题中，常常用到这个经验公式：感应电量
，常用来求位移．但在计算题中，不能直接作为公式用，要推导。
本题难度：一般
4、简答题 如图甲所示,两根足够长的平行光滑金属导轨固定放置在水平面上，间距L＝0.2m，一端通过导线与阻值为R=1Ω的电阻连接；导轨上放一质量为m＝0.5kg的金属杆，金属杆与导轨的电阻均忽略不计.整个装置处于竖直向上的大小为B＝0.5T的匀强磁场中.现用与导轨平行的拉力F作用在金属杆上，金属杆运动的v-t图象如图乙所示.（取重力加速度g=10m/s2）求：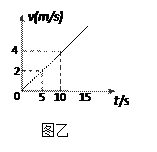
（1）t＝10s时拉力的大小及电路的发热功率.
（2）在0～10s内，通过电阻R上的电量.
?
参考答案：（1）0.16W?（2）2C
本题解析：(1)由v-t图象可知：
? ①
由牛顿第二定律:
? ② 
? ③?
? ④
? ⑤?
（或由图可知，t=10s时，v=4m/s） ⑥
联立以上各式，代入数据得：
＝0.24N? ⑦
?⑧
(2)
?⑨
?⑩?
?⑾?
? ⑿
联立以上各式，代入数据得:
? ⒀
本题难度：简单
5、简答题 如图所示，一边长为a的正方形导线框内有一匀强磁场，磁场方向垂直于导线框所在平面向内，导线框的左端通过导线接一对水平放置的金属板，两板间的距离为d，板长l=3d．t=0时，磁场的磁感应强度从B0开始均匀增加，同时，在金属板的左侧有一质量为m、电荷量为q的带正电粒子以大小为v0的初速度沿两板间的中线向右射入两板间，恰好从下板的边缘射出，忽略粒子的重力作用．求：
（1）粒子在板间运动过程，两板间的电势差．
（2）粒子从两板间离开瞬间，磁感应强度B的大小．
参考答案：（1）粒子在板间做类平抛运动，水平方向做匀速直线运动，竖直方向做初速度为零的匀加速运动，则有
水平方向：l=3d=v0t
竖直方向：d2=12at2，
又a=qUmd
联立解得，两板间的电势差U=mv209q
（2）根据法拉第电磁感应定律得
U=△Φ△t=a2△B△t
根据楞次定律可知，磁感应强度B应均匀增大，有
△B△t=B-B0t
又t=3dv0
联立解得，粒子从两板间离开瞬间，磁感应强度B的大小为B=B0+mv0d3qa2
答：（1）粒子在板间运动过程，两板间的电势差是mv209q．
（2）粒子从两板间离开瞬间，磁感应强度B的大小是B0+mv0d3qa2．
本题解析：
本题难度：一般