时间:2017-07-31 07:52:21
1、计算题 如图所示,长度为L=1.0m的绳,系一小球在竖直面内做圆周运动,小球的质量为M=5kg,小球半径不计,不考虑空气阻力,小球在通过最低点的速度大小为v=8m/s。试求:(g=10m/s2)
(1)小球在最低点的向心加速度的大小;
(2)小球在最低点受到的向心力的大小;
(3)小球在最低点所受绳的拉力的大小。 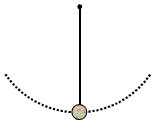
参考答案:解:(1)向心加速度为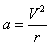
代入数据得a = 64 m/s2
(2)由牛顿第二定律得向心力为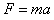
代入数据得F=320N
(3)绳的拉力为T=F+G =370N
本题解析:
本题难度:一般
2、选择题 开口向上的半球形曲面的截面如图所示,直径AB水平。一小物块在曲面内A点以某一速率开始下滑,曲面内各处动摩擦因数不同,因摩擦作用物块下滑时速率不变,则下列说法正确的是
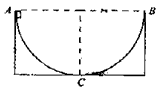
[? ]
参考答案:B
本题解析:
本题难度:一般
3、计算题 如图所示,质量为0.1kg的木桶内盛0.4kg水后,用50cm长的绳子系在桶上使它在竖直面内做圆周运动。如果它通过最高点和最低点时的速度分别为9m/s和10m/s,求木桶在最高点和最低点对绳的拉力及水对桶底的压力。(取g=10m/s2)
参考答案:76N,60.8N,105N,84N
本题解析:
本题难度:一般
4、选择题 a、b两辆玩具车在各自的圆轨道上做匀速圆周运动,在相同的时间内,它们通过的路程之比为3:4,运动方向改变的角度之比为2:3,则它们的向心加速度大小之比为
[? ]
参考答案:B
本题解析:
本题难度:简单
5、简答题 如图所示,一条轨道固定在竖直平面内,粗糙的ab段水平,bcde段光滑,cde段是以O为圆心、R为半径的一小段圆弧.可视为质点的物块A和B紧靠在一起,静止于b处,A的质量是B的3倍.两物块在足够大的内力作用下突然分离,分别向左、右始终沿轨道运动.B到d点时速度沿水平方向,此时轨道对B的支持力大小等于B所受重力的
| 3 4 |
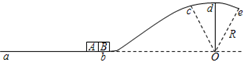
参考答案:(1)B在d点,根据牛顿第二定律有:mg-34mg=mv2R?解得:v=
本题解析:
本题难度:一般