时间:2017-07-31 07:32:47
1、选择题 如图所示，在匀强磁场中有一倾斜的平行金属导轨，导轨间距为l，两导轨间连有一电阻R，导轨平面与水平面的夹角为θ，在两虚线间的导轨上涂有薄绝缘涂层．匀强磁场的磁感应强度大小为B，方向与导轨平面垂直．质量为m的导体棒从h高度处由静止释放，在刚要滑到涂层处时恰好匀速运动．导体棒始终与导轨垂直且仅与涂层间有摩擦，动摩擦因数μ=tanθ，其他部分的电阻不计，重力加速度为g，下列说法正确的是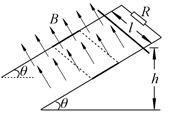
A．导体棒到达涂层前做加速度减小的加速运动
B．在涂层区导体棒做减速运动
C．导体棒到达底端的速度为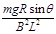
D．整个运动过程中产生的焦耳热为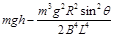
参考答案：AC
本题解析：导体棒到达涂层前随着速度的增加，安培力越来越大，因此合力越来越小，加速度越来越小，因此做加速度减小的加速运动，A正确；由于到达涂层时已匀速运动，而涂层的动摩擦因数μ=tanθ，因此在涂层区导体棒做匀速运动，B错误；穿过涂层后导体棒仍匀速运动，因此到达底端时，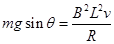
，因此导体棒到达底端的速度为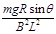，C正确，由于涂层存在，因此整个运动过程中产生的焦耳热为
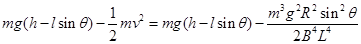，其中l为涂层的宽度，D错误。
考点：电磁感应，功能关系
本题难度：困难
2、选择题 如图所示，一导线AC以速度υ在金属轨道DFEF上匀速滑动，向右通过一匀强磁场，金属轨道EF间有电阻R，其余的电阻不计，则在通过此匀强磁场的过程中，下列物理量中与速度υ成正比的是：（ ）
①导线AC中的感应电流强度
②磁场作用于导线AC上的磁场力
③电阻R上所产生的电热
④电阻R上所消耗的电功率．
A．①②
B．①③
C．②④
D．③④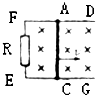
参考答案：①AC产生的感应电动势 E=BLv，感应电流为 I=ER=BLvR∝v，故①正确．
②磁场作用于导线AC上的磁场力：F=BIL=B2L2Rv∝v，故②正确．
③根据能量转化和守恒定律得知，电阻R上所产生的电热为 Q=Fs=B2L2Rvs∝v，故③正确．
④电阻R上所消耗的电功率：P=E2R=(BLv)2R∝v2，故④错误．
故选：AB
本题解析：
本题难度：简单
3、选择题 如图所示，用一根横截面积为s的硬导线做成一个半径为r的圆环，把圆环部分置于均匀变化的匀强磁场中，磁场方向垂直纸面向里，磁感应强度大小随时间的变化率style="shiti/data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAABkAAAAoCAIAAACErcY8AAAAkklEQVRIie2UwQ6AIAxD+/8/rQeMMbCOuY15wJ6AjGeRURx5ws8KsQA/fRmrgXQcBvlZz8puLCxZrInTKEs447hZwYk/y8NiB7xYxm21LN+VselcrLT/sGLqrbZgZSnbVwVL7+GPWDAHbA7L9IZAYnMVS3ze8zhVcBNfRpa86LRQx7J3AOsYmr8sDO5izVdcO7BOH3AiawwJmUwAAAAASUVORK5CYII=" alt="">=k（k＞0），ab为圆环的一条直径，导线的电阻率为ρ。则（? ）
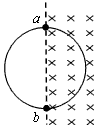
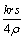
参考答案：C
本题解析：
本题难度：一般
4、计算题 如图所示，两根足够长的平行光滑金属导轨MN、PQ间距为d,其电阻不计，两导轨所在的平面与水平面成θ角。质量分别为m和3m，电阻均为R的两金属棒ab、cd分别垂直导轨放置，每棒两端都与导轨始终有良好接触，两棒之间用一绝缘的细线相连，整个装置处在垂直于导轨平面向上的匀强磁场中，磁感应强度为B，给棒ab施加一平行于导轨向上的拉力作用，使两棒均保持静止。若在t=0时刻将细线烧断，此后保持拉力不变，重力加速度为g。
(1)细线烧断后，当ab棒加速度为a1时，求cd棒的加速度大小a2 (用a1表示)；
(2)求ab棒最终所能达到的最大速度。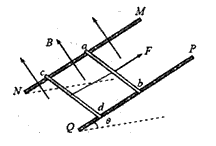 
参考答案：解：（1）烧断细线前拉力设为 ，则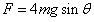
烧断细线后，对ab棒，设此时ab棒所受安培力的大小为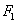
,由牛顿第二定律得：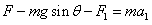 
同时，设cd棒此时所受安培力的大小为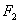
，由牛顿第二定律得：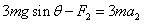 
且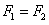
由以上各式解得：
；
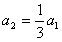（2）当ab棒和cd棒加速度为零时，速度均达最大, 设此时ab棒和cd棒的速度大小分别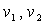
由cd棒受力平衡：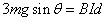
此时回路中总的电动势：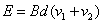
电路中电流：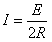
由动量守恒定律：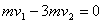
由以上各式解得：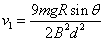
本题解析：
本题难度：一般
5、简答题 如图甲所示，某人设计了一种振动发电装置，它的结构是一个半径r=0.1m、20匝的线圈套在辐向形永久磁铁槽中，磁场中的磁感线均沿半径方向均匀分布，从右侧观察如图乙所示．已知线圈所在位置磁感应强度B的大小均为0.2T，线圈总电阻为2Ω，它的引出线接有阻值为8Ω的灯泡L．外力推动与线圈相连的P端使其做往复运动，线圈切割辐向磁场中的磁感线产生感应电流，线圈位移随时间变化的规律如图丙所示（线圈位移取向右为正）．
（1）在丁图中画出感应电流随时间变化的图象（在乙图中取逆时针电流为正＞；
（2）求每一次推动线圈运动过程中作用力的大小；
（3）若不计摩擦等损耗，求该发电机的输出功率．
参考答案：（1）从图中可以看出，线圈往返的每次运动都是匀速直线运动，其速度为：v=△x△t=0.080.1m/s=0.8m/s．
线圈做切割磁感线运动产生的感应电动势：E=n2πrBv=20×2×3.14×0.1×0.2×0.8V=2V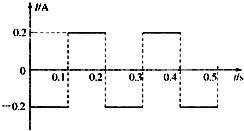
感应电流：I=Er+R=210=0.2A．
根据右手定则可得，当线圈沿x正方向运动时，产生的感应电流在图1（a）中是由D向下经过电珠L流向C的．于是可得到如答图所示的电流随时间变化的图象．
（2）由于线圈每次运动都是匀速直线运动，所以每次运动过程中推力必须等于安培力．F推=F安=nILB=nI（2πr）B=20×0.2×2×3.14×0.1×0.2=0.5N．
（3）发电机的输出功率即灯的电功率．P=I2R=（0.2）2×8W=0.32W
答：（1）感应电流随时间变化的图象如图所示．
（2）每一次推动线圈运动过程中的作用力是0.5N．
（3）该发电机输出的功率0.32W．
本题解析：
本题难度：一般