时间:2017-07-27 12:09:44
1、选择题 如图所示,在光滑水平面上,质量为m的小球在细线的拉力作用下,以速度υ做半径为r的匀速圆周运动.小球所受向心力的大小为( )
A.m
| v2 r |
| v r |

参考答案:根据牛顿第二定律得,小球的向心力由细线的拉力提供,则有:
F=mv2r.故A正确,B、C、D错误.
故选:A.
本题解析:
本题难度:简单
2、简答题 图1所示为一根竖直悬挂的不可伸长的轻绳,下端栓一小物块A,上端固定在C点且与一能测量绳的拉力的测力传感器相连.已知有一质量为m0的子弹B沿水平方向以速度v0射入A内(未穿透),接着两者一起绕C点在竖直面内做圆周运动.在各种阻力都可忽略的条件下测力传感器测得绳的拉力F随时间t的变化关系如图2所示.已知子弹射入的时间极短,且图2中t=0为A、B开始以相同速度运动的时刻.根据力学规律和题中(包括图)提供的信息,对反映悬挂系统本身性质的物理量(例如A的质量)及A、B一起运动过程中的守恒量,你能求得哪些定量的结果?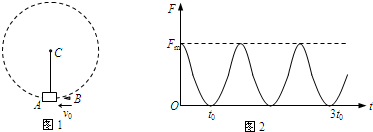
参考答案:由图2可直接看出,A、B一起做周期性运动,运动周期为T=2t0.用m、m0分别表示A、B的质量,l表示绳长,v1、v2分别表示它们在圆周最低、最高点的速度,F1、F2分别表示运动到最低、最高点时绳的拉力大小;
子弹射入木块过程,根据动量守恒定律,有
m0v0=(m+m0)v1? ①
根据牛顿定律有:
最低点? F1-(m+m0)g=(m+m0)v21l? ②
最高点? F2+(m+m0)g=(m+m0)v22l? ③
由机械能守恒又有:
(m+m0)g?(2l)=12(m+m0)v12-12(m+m0)v22? ④
由图2知,F2=0,F1=Fm,由以上各式解得,反映系统本身性质的物理量是
木块质量? m=Fm6g-m0
细线长度? l=36m20v205F2mg
以最低点所在的水平面为参考平面,系统总机械能是
E=12(m+m0)v12 ⑤
解得
E=3m20v20gFm
故可以求出A的质量为Fm6g-m0,细线长度为36m20v205F2mg,A、B一起运动过程中的守恒量为机械能,以最低点所在的水平面为参考平面,总机械能为3m20v20gFm.
本题解析:
本题难度:一般
3、选择题 如图所示,有一质量为M的大圆环,半径为R,被一轻杆固定后悬挂在O点,有两个质量为m的小环(可视为质点),同时从大环两侧的对称位置由静止滑下。两小环同时滑到大环底部时,速度都为v,则此时大环对轻杆的拉力大小为 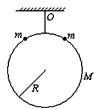
[? ]
A.(2m+2M)g
B.Mg-2mv2/R
C.2m(g+v2/R)+Mg
D.2m(v2/R-g)+Mg
参考答案:C
本题解析:
本题难度:一般
4、选择题 竖直平面内固定一内壁光滑半径为r的圆形细弯管,如图所示.管内有一质量为m,直径很小的小球(可视为质点)做圆周运动,小球在最高点时,恰与管壁无相互作用力,则小球通过最低点时管壁对小球的作用力大小为( )
A.4mg
B.5mg
C.6mg
D.7mg
参考答案:设小球通过轨道最高点时速度的大小为v1,根据题意和圆周运动向心力公式得:
? mg=mv12r
解得:v1=
本题解析:
本题难度:简单
5、简答题 如图所示,质量为m的小球,由长为l的细线系住,细线的另一端固定在A点,AB是过A的竖直线,E为AB上的中点,过E作水平线EF,在EF上钉铁钉D,现将小球拉直水平,然后由静止释放,小球在运动过程中,不计细线与钉子碰撞时的能量损失,不考虑小球与细线间的碰撞.
(1)若钉铁钉位置在E点,求细线与钉子碰撞前后瞬间,细线的拉力分别是多少?
(2)若小球恰能绕钉子在竖直面内做完整的圆周运动,求钉子位置D在水平线EF上距E点的距离ED的值是多少?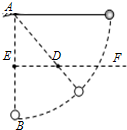
参考答案:(1)小球从M点到B点的过程中,根据动能定理得:
? mgl=12mv2
碰前:T1-mg=mv2l
解得:T1=3mg
细线与钉子碰撞前后小球的速度大小不变,则碰后瞬间:
T2-mg=mv212l
解得:T2=5mg
(2)设D距E的距离为x.随着x的增大,绕钉子做圆周运动的半径越来越小,根据机械能守恒定律知,转至最高点的瞬时速度越来越大,当这个瞬时速度大于或等于临界速度时,小球就能到达圆的最高点了.
设钉子在D点小球刚能绕钉子做圆周运动到达圆的最高点,设ED=x.
? 则AD=
本题解析:
本题难度:一般