时间:2017-07-27 12:06:02
1、选择题 如图所示,质量为m、电荷量为q的带电液滴从h高处自由下落,进入一个互相垂直的匀强电场和匀强磁场区域,磁场方向垂直纸面,磁感应强度为B,电场强度为E。已知液滴在此区域中做匀速圆周运动,则圆周运动的半径R为(?)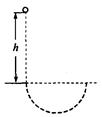
A.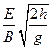
B.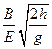
C.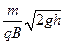
D.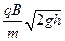
2、选择题 关于带电粒子在匀强电场和匀强磁场中的运动,下列说法中正确的是( )
A.带电粒子沿电场线方向射入,电场力对带电粒子做正功
B.带电粒子垂直于电场线方向射入,电场力对带电粒子不做功
C.带电粒子沿磁感线方向射入,洛伦兹力对带电粒子做正功
D.不管带电粒子怎样射入磁场,洛伦兹力对带电粒子都不做功
3、计算题 (10分)如图所示,两根平行且光滑的金属轨道固定在斜面上,斜面与水平面之间的夹角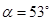 ,轨道上端接一只阻值为R=0.4
,轨道上端接一只阻值为R=0.4 的电阻器,在导轨间存在垂直于导轨平面的匀强磁场,磁场的磁感应强度B=0.5 T,两轨道之间的距离为L=40cm,且轨道足够长,电阻不计。现将一质量为m="3" g,有效电阻为r=1.0
的电阻器,在导轨间存在垂直于导轨平面的匀强磁场,磁场的磁感应强度B=0.5 T,两轨道之间的距离为L=40cm,且轨道足够长,电阻不计。现将一质量为m="3" g,有效电阻为r=1.0 的金属杆ab放在轨道上,且与两轨道垂直,然后由静止释放,求:
的金属杆ab放在轨道上,且与两轨道垂直,然后由静止释放,求: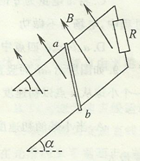
(1)金属杆ab下滑过程中可达到的最大速率;
(2)金属杆ab达到最大速率以后,电阻器R每秒内产生的电热。
4、选择题 如图所示空间存在着竖直向上的匀强电场和垂直纸面向外的匀强磁场,一带电液滴从静止开始自A沿曲线ACB运动到B点时,速度为零,C是轨迹的最低点,以下说法中不正确的是(?)
A.滴带负电
B.滴在C点动能最大
C.若液滴所受空气阻力不计,则机械能守恒
D.液滴在C点机械能最大
5、选择题 如图所示为一速度选择器,内有一磁感应强度为B,方向垂直纸面向外的匀强磁场,一束粒子流以速度v水平射入,为使粒子流经磁场时不偏转(不计重力),则磁场区域内必须同时存在一个匀强电场,关于这个电场场强大小和方向的说法中正确的是 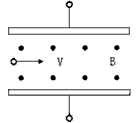
[? ]
A.大小为B/v,粒子带正电时,方向向上
B.大小为B/v,粒子带负电时,方向向下
C.大小为Bv,方向向下,与粒子带何种电荷无关
D.大小为Bv,方向向上,与粒子带何种电荷无关