时间:2017-07-27 12:00:06
1、选择题 设洒水车的牵引力不变,所受阻力与车重成正比.洒水车在平直路面上行驶,原来是匀速的,开始洒水后,它的运动情况将是
A.继续做匀速运动
B.变为做匀加速运动
C.变为做变加速运动
D.变为做匀减速运动
2、选择题 如图所示,在托盘测力计的托盘内固定一个倾角为30°的光滑斜面,现将一个重4N 的物体A 放在斜面上,让它自由滑下,那么测力计因物体A 的自由滑下而变化的读数是(取g=10m/s2)
A.0
B.3N
C.1N
D.2N
3、选择题 做斜抛运动的物体到达最高点时
A.速度为零
B.竖直分速度为零
C.合力为零
D.加速度为零
4、选择题 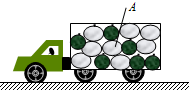 如图所示,有一辆汽车满载西瓜在水平路面上向左匀速前进.突然发现意外情况,紧急刹车做匀减速运动,加速度大小为a,则中间一质量为m的西瓜A受到其他西瓜对它的作用力的合力的大小和方向是
如图所示,有一辆汽车满载西瓜在水平路面上向左匀速前进.突然发现意外情况,紧急刹车做匀减速运动,加速度大小为a,则中间一质量为m的西瓜A受到其他西瓜对它的作用力的合力的大小和方向是
A.ma水平向左
B.ma水平向右
C.斜向右上方
D.斜向左上方
5、选择题 对于牛顿第三定律的理解,下列说法正确的是
A.当作用力产生后,再产生反作用力;当作用力消失后,反作用力才慢慢消失
B.弹力和摩擦力都有反作用力,而重力无反作用力
C.甲物体对乙物体的作用力是弹力,乙物体对甲物体的作用力可以是摩擦力
D.作用力和反作用力,这两个力在任何情况下都不会平衡