时间:2017-07-27 11:56:25
1、计算题 如图所示,在xoy平面的第一象限有匀强电场,电场方向沿-y方向。在 x轴的下方存在着垂直于xoy平面的匀强磁场,磁感应强度为B。有一质量为m、电荷量为q的正电荷从y轴上的A点以平行于x轴的速度射入电场中,从x轴上的B点进入磁场中。电荷在B点时的速度与x轴的夹角为α,BO=L,粒子最后从坐标原点射出磁场。求:
(1)粒子在磁场中运动的时间为多少?
(2)粒子在磁场中运动的速度大小?
(3)电场强度的大小?
参考答案:解:(1)解: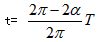
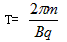 ,解得:
,解得: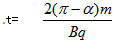
(2)2r sinα=L?, r=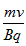
解得: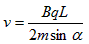
(3)vx=vcosα?,vsinα= 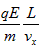
解得:E=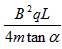
本题解析:
本题难度:困难
2、计算题 如图甲所示,在真空中,有一半径为R的圆形区域内存在匀强磁场,磁场方向垂直纸面向外。在磁场右侧有一对平行金属板M和N,两板间距为R,板长为2R,板间的中心线O1O2与磁场的圆心O在同一直线上。有一电荷量为q、质量为m的带正电的粒子以速度v0从圆周上的a点沿垂直于半径OO1并指向圆心O的方向进入磁场,当从圆周上的O1点水平飞出磁场时,给M、N两板加上如图乙所示的电压,最后粒子刚好以平行于N板的速度从N板的边缘飞出。(不计粒子所受到的重力、两板正对面之间为匀强电场,边缘电场不计),求:
(1)磁场的磁感应强度B;
(2)求交变电压的周期T和电压U0的值;
(3)当t=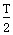 时,该粒子从M、N板右侧沿板的中心线仍以速度v0射入M、N之间,求粒子从磁场中射出的点到a点的距离。
时,该粒子从M、N板右侧沿板的中心线仍以速度v0射入M、N之间,求粒子从磁场中射出的点到a点的距离。 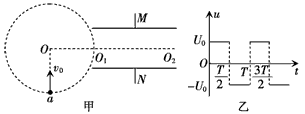
参考答案:解:(1)粒子自a点进入磁场,从O1点水平飞出磁场,则其运动的轨道半径为R
由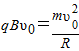 ,解得:
,解得: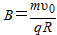
(2)粒子自O1点进入电场后恰好从N板的边缘平行极板飞出,设运动时间为t,根据类平抛运动规律有: 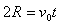 ,
,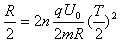
又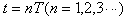
解得: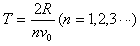 ,
,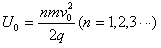
(3)当t=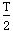 时,粒子以速度v0沿O2O1射入电场,该粒子恰好从M板边缘以平行于极板的速度射入磁场,进入磁场的速度仍为v0,运动的轨迹半径为R。设进入磁场时的点为b,离开磁场时的点为c,圆心为O3,如图所示,四边形ObO3c是菱形,所以Oc∥O3b,故c、O、a三点共线,ca即为圆的直径,则c、a间的距离d=2R
时,粒子以速度v0沿O2O1射入电场,该粒子恰好从M板边缘以平行于极板的速度射入磁场,进入磁场的速度仍为v0,运动的轨迹半径为R。设进入磁场时的点为b,离开磁场时的点为c,圆心为O3,如图所示,四边形ObO3c是菱形,所以Oc∥O3b,故c、O、a三点共线,ca即为圆的直径,则c、a间的距离d=2R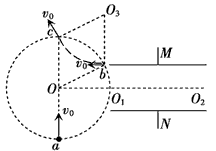
本题解析:
本题难度:困难
3、计算题 如图所示,有一半径为R1=1 m的圆形磁场区域,圆心为O,另有一外半径为R2= m、内半径为R1的同心环形磁场区域,磁感应强度大小均为B=0.5 T,方向相反,均垂直于纸面,一带正电粒子从平行极板下板P点静止释放,经加速后通过上板小孔Q,垂直进入环形磁场区域,已知点P、Q、O在同一竖直线上,上极板与环形磁场外边界相切,粒子比荷q/m=4×107 C/kg,不计粒子的重力
m、内半径为R1的同心环形磁场区域,磁感应强度大小均为B=0.5 T,方向相反,均垂直于纸面,一带正电粒子从平行极板下板P点静止释放,经加速后通过上板小孔Q,垂直进入环形磁场区域,已知点P、Q、O在同一竖直线上,上极板与环形磁场外边界相切,粒子比荷q/m=4×107 C/kg,不计粒子的重力 ,且不考虑粒子的相对论效应,求:
,且不考虑粒子的相对论效应,求:
(1)若加速电压U1=1.25×102 V,则粒子刚进入环形磁场时的速度v0多大?
(2)要使粒子不能进入中间的圆形磁场区域
 ,加速电压U2应满足什么条件?
,加速电压U2应满足什么条件?
(3)若改变加速电压大小,可使粒子进入圆形磁场区域,且能水平通过圆心O,最后返回到出发点,则粒子从Q孔进入磁场到第一次经过O点所用的时间为多少?
参考答案:(1)1×105 m/s
(2)U 2≤5×106 V
2≤5×106 V
(3)1.83×10- 7 s
7 s
本题解析:
本题难度:困难
4、选择题 带电质点在匀强磁场中运动,某时刻速度方向如图所示,所受的重力和洛伦兹力的 合力恰好与速度方向相反,不计阻力,则在此后的一小段时间内,带电质点将
合力恰好与速度方向相反,不计阻力,则在此后的一小段时间内,带电质点将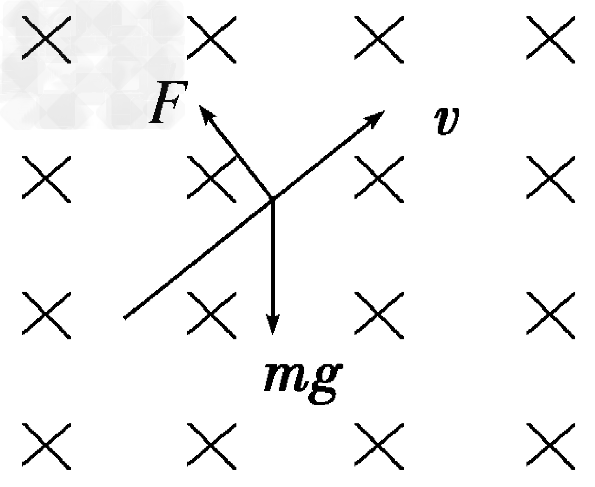
[? ]
A.可能做直线运动
B.可能做匀减速运动
C.一定做曲线运动
D.可能做匀速圆周运动
参考答案:C
本题解析:
本题难度:一般
5、计算题 如图所示,在xOy平面的第一象限有一匀强电场,电场强度大小未知,电场的方向平行于y轴向下;在x轴和第四象限的射线OC之间有一匀强磁场,磁感应强度的方向垂直于纸面向外。有一质量为m,带有电荷量+q的质点由电场左侧平行于x轴射入电场。质点到达x轴上A点时,速度大小为v,速度方向与x轴的夹角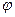 ,A点与原点O的距离为d。接着质点进入磁场,并垂直于磁场边界的OC射线飞离磁场。不计重力影响。若OC与x轴的夹角为
,A点与原点O的距离为d。接着质点进入磁场,并垂直于磁场边界的OC射线飞离磁场。不计重力影响。若OC与x轴的夹角为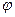 ,求
,求
(1)磁感应强度B的大小
(2)匀强电场的场强E的大小。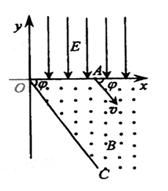
参考答案:(1)B=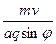
(2)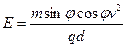
本题解析:略
本题难度:简单