时间:2017-07-27 11:56:25
1、计算题 如图所示，高h=0.8m的绝缘水平桌面上方的区域Ⅰ中存在匀强电场，场强E 的方向与区域的某一边界平行，区域Ⅱ中存在垂直于纸面的匀强磁场B。现有一质量m=0.01kg，带电荷量q=+10-5C的小球从A点以v0=4m/s的初速度水平向右运动，匀速通过区域Ⅱ后落在水平地面上的B点，已知：小球与水平桌面间的动摩擦因数，L=1m，h=0.8m，x=0.8m，取g=10m/s2。试求：
（1）小球在区域Ⅱ中的速度；
（2）区域Ⅱ中磁感应强度B的大小及方向；
（3）区域Ⅰ中电场强度E的大小及方向。 
参考答案：解：（1）小球离开磁场后做平抛运动，设小球在磁场中匀速运动的速度为v，则有
①?
②
联立①②解得：
③
（2）由于小球在磁场中作匀速运动，所以小球不可能受摩擦力作用，也就不受桌面的弹力（支持力）作用，只能受重力和洛仑兹力作用，且
④
又
⑤
联立④⑤解得：
⑥
代入数值得：
⑦
根据左手定则可判断磁感应强度B的方向垂直纸面向里。
（3）由于v＜v0，所以小球在电场中作减速运动。电场方向有两种可能
（i）电场方向水平向左。小球在电场中，由动能定理：
⑧
解得：
⑨
（ii）电场方向沿竖直方向，设竖直向上。
小球在电场中，由动能定理：
⑩
解得：
“－”号表示E的方向与假设方向相反，即竖直向下。
本题解析：
本题难度：困难
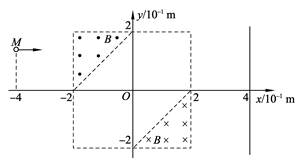
2、简答题 ）如图所示，在直角坐标系的第Ⅱ象限和第Ⅳ象限中的直角三角形区域内，分布着磁感应强度均为B＝5.0×10－2T的匀强磁场，方向分别垂直纸面向外和向里。质量为m＝6.64×10－27kg、电荷量为q＝＋3.2×10－19C的α粒子（不计α粒子重力），由静止开始经加速电压为U＝1 205 V的电场（图中未画出）加速后，从坐标点M（－4，2）处平行于x轴向右运动，并先后通过匀强磁场区域。
参考答案：（1）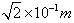
（2）图见解析 （3）6.5×10-7 s
本题解析：（1） α粒子在电场中被加速，由动能定理得qU="1/2" mv2（3分）
α粒子在磁场中偏转，则牛顿第二定律得qvB=mv2/r（2分）
联立解得
（1分）
（2） 能正确作出图象得（6分）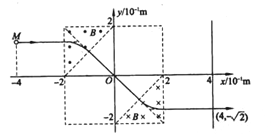
（3） 带电粒子在磁场中的运动周期
T=2πr/v=2πm/qB（2分）
α粒子在两个磁场中偏转的角度均为π/4，在磁场中的运动总时间
t="1/4" T=πm/2qB=（3.14×6.64×10-27）/（2×3.2×10-19×5×10-2）=6.5×10-7 s（3分）
本题难度：一般
3、选择题 如图所示，平行板间有正交的匀强电场E和匀强磁场B，一带电粒子（不计重力）沿垂直于B、E的方向射入，从平行板间射出时动能减少，为了使带电粒子在平行板间运动时动能增加，可采用下列哪些方法（ ）
A．增加进入时粒子的速
B．使磁场的磁感应强度B增加
C．改变粒子带电性质
D．使两板间电压U增加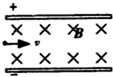
参考答案：
无论粒子带何种电荷，由于电场力与洛伦兹力都是方向相反的，而动能减少说明电场力做了负功，即电场力小于洛伦兹力，粒子向洛伦兹力的方向偏转了．所以要使动能增大，必然减小磁场力或增大电场力．?
A：增大速度，则磁场力增大而电场力不变，动能更会减少．选项A错误；
B：增大磁感应强度即增大了洛伦兹力，不符合上面的分析．选项B错误；
C：改变电性，两力同时反向，磁场力仍大于电场力，所以粒子动能仍会减少．选项C错误；
D：若使两板电压增加，则增加电场强度，即增大电场力，使粒子向电场力方向偏转，这样电场力做正功，所以动能会增大．选项D正确．
故选：D
本题解析：
本题难度：一般
4、选择题 如图所示，在Oxyz坐标系所在的空间中，可能存在着匀强电场E或匀强磁场B，也可能两者都存在。现有一质量为m、电荷量为q的正点电荷沿z轴正方向射入此空间，发现它做速度为v0的匀速直线运动，若不计此点电荷的重力，则下列关于电场E和磁场B的分布情况中有可能的是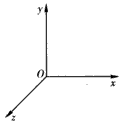
[? ]
A．E≠0，B=0，且E沿z轴正方向或负方向
B．E=0，B≠0，且B沿z轴正方向或负方向
C．E≠0，B≠0，B沿x轴正方向，E沿y轴正方向
D．E≠0，B≠0，B沿x轴正方向，E沿y轴负方向
参考答案：B
本题解析：
本题难度：一般
5、简答题 长为L的水平极板间，有垂直纸面向里的匀强磁场，如图所示，磁感应强度为B，板间距离也为L，板不带电，现有质量为m、电量为q的正电粒子（不计重力），从左边极板间中点处垂直磁感线以初速度v水平射入磁场，欲使粒子不打在极板上，求初速度v的范围．
参考答案：如图所示：
由题意知，带正电的粒子从左边射出磁场，其在磁场中圆周运动的半径R＜L4；
因为粒子在磁场中做圆周运动洛伦兹力提供向心力即：
qvB=mv2R
可得粒子做圆周运动的半径：
R=mvqB
粒子从左边射出，则：
mvqB＜L4，即v＜qBL4m
带正电的粒子不从右边射出，如图所示，此时粒子的最大半径为R，由上图可知：
R2=L2+（R-L2）2
可得粒子圆周运动的最大半径：
R=5L4
又因为粒子做圆周运动，洛伦兹力提供向心力，粒子不从右边射出，则：
mvqB＞5L4
即此时v＞5qBL4m
所以粒子不从磁场区域射出速度满足：v＜qBL4m或者v＞5qBL4m．
答：初速度v的范围：v＞5qBL4m或v＜qBL4m．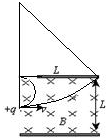
本题解析：
本题难度：一般