时间:2017-07-17 08:16:49
1、简答题 如图所示,为某游戏装置的示意图.高处的光滑水平平台上有一质量为m的滑块(可视为质点)静止在A点,平台的左端有一竖直固定的光滑半圆形细管BC,其半径为2R,与水平面相切于C点,CD为一段长度为5R的粗糙水平轨道,在D处有一竖直固定的半径为R的光滑四分之一圆弧轨道DE,E点切线竖直,在E点正上方有一离E点高度也为R的旋转平台,在旋转平台的一条直径上开有两个离轴心距离相等的小孔M、N,平台以恒定的角速度旋转时两孔均能经过E点的正上方.某游戏者在A点将滑块瞬间弹出,滑块第一次到达C点时速度为v0=3
| gR |

参考答案:(1)从A点到C点,由动能定理得到:
W+mg?4R=12mv20
解得:W=0.5mgR
(2)从第一次经过C点到第一次返回C点的整个过程,根据动能定理,有:
-2μmg?5R=12mv2C-12mv20
在C点,由牛顿第二定律,得到:
FN-mg=mv2C2R
联立解得:FN=4.5mg,方向竖直向下
(3)从第一次经过C点到M点,由动能定理,得:
-2μmg?5R-mg?2R=12mv2M-12mv2C
从点M落回到点N的时间为:t=2vMg
对转盘,有:t=(2n+1)πω (n=0、1、2、…)
联立求解得:ω=(2n+1)π
本题解析:
本题难度:一般
2、选择题 一个人站在高出地面h处,抛出一个质量为m的物体,物体落地时速率为v,空气阻力可以忽略不计,则人对物体所做的功为
A.mgh
B.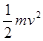
C.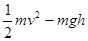
D.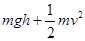
参考答案:C
本题解析:设人对物体所做的功为W,根据动能定理得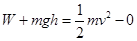
得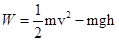 ,故选C
,故选C
点评:本题应用动能定理分析多过程问题,采用的是全程法,也可以采用分段法处理,分成人抛物体过程和物体飞行过程分别用动能定理研究.
本题难度:一般
3、计算题 如图所示,在场强E=104 N/C的水平匀强电场中,有一根长l=15 cm的细线,一端固定在O点,另一端系一个质量m=3 g、电荷量q=2×10-6 C的带正电小球,当细线处于水平位置时,小球从静止开始释放,则小球到达最低点B的速度是多大?(取g=10 m/s2) 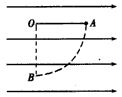
参考答案:解:小球在下落过程中,重力做正功,电场力做负功
WG=mg·OB=mgl =3×10-3 kg×10 N/kg×0.15 m=4.5×10-3 J
W电=- qE·OA=- qEl=-2×10-6 C×104 N/C×0.15 m=-3×10-3 J
根据动能定理W=WG+W电=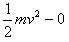
解得:v=1 m/s
本题解析:
本题难度:一般
4、选择题 一质量为m的小球,用长为L的轻绳悬挂于O点,小球?在水平力F作用下,从平衡位置P很缓慢地移动到Q点,如图所示,则力F所做的功为( )
A.mgLcosθ
B.mgL(1-cosθ)
C.FLsinθ
D.FL(1-cosθ)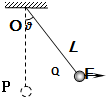
参考答案:对小球受力分析,受到重力、拉力F和绳子的拉力T,如图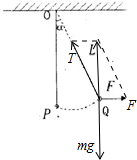
根据共点力平衡条件,有
F=mgtanα,故F随着α的增大而不断变大,故F是变力;
对小球运动过程运用动能定理,得到
-mgL(1-cosα)+W=0
故拉力做的功等于mgL(1-cosθ)
故选B.
本题解析:
本题难度:简单
5、简答题 如图所示,半径为R的光滑绝缘圆环固定在竖直平面内,在环的底端B点固定一个带正电的小球,环上还套有一个质量为m,带等量正电荷的小球,现将小球从A点(半径OA水平)由静止释放开始运动,当运动到C点(∠AOC=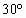 )时获得的最大动能为Ekm,求:
)时获得的最大动能为Ekm,求: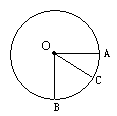
(1)小球从位置A运动到位置C的过程中所受静电力做的功W;
(2)小球在A点刚释放时运动的加速度a;
(3)小球在位置C时受到圆环对它的作用力.
参考答案:
(1)Ekm-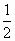 mgR.?(2)(1-
mgR.?(2)(1-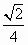 )g (3) mg+2Ekm/R.
)g (3) mg+2Ekm/R.
本题解析:(1)由A→C根据动能定理m gRsin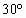 +
+ =Ekm,
=Ekm,
得 =Ekm-
=Ekm-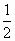 mgR.
mgR.
(2)由C点受力平衡,可判定mg= ,
,
又∵ 无穷趋近于
无穷趋近于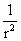 ,∴
,∴ =
=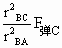 =
=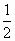 mg.
mg.
又∵vA=0,∴a=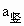 =(mg-
=(mg- cos
cos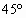 )/m
)/m
=(1-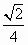 )g.
)g.
(3)在C点 与mg的合力恰好为mg,方向沿OC.
与mg的合力恰好为mg,方向沿OC.
N-mg=mv2/R,得N=mg+2Ekm/R.
本题难度:一般