时间:2017-03-05 17:01:02
1、选择题 如图所示,质量为m、电荷量为q的带电液滴从h高处自由下落,进入一个互相垂直的匀强电场和匀强磁场区域,磁场方向垂直于纸面,磁感应强度为B,电场强度为E.已知液滴在此区域中做匀速圆周运动,则圆周运动的半径r为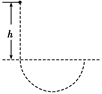
A.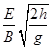
B.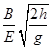
C.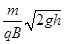
D.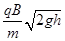
2、选择题 在同时存在匀强电场和匀强磁场的空间中取正交坐标系Oxyz(y轴正方向竖直向上),如图所示。已知电场方向沿y轴正方向,场强大小为E;磁场方向沿z轴正方向,磁感应强度的大小为B;重力加速度为g。一质量为m、带电量为+q的带电微粒从原点以速度v出发。关于它在这一空间的运动的说法正确的是

[? ]
3、选择题 环形对撞机是研究高能粒子的重要装置,其核心部件是一个高度真空的圆环状的空腔。若带电粒子初速度可视为零,经电压为U的电场加速后,沿圆环切线方向注入对撞机的环状腔内,空腔内存在着与圆环平面垂直的匀强磁场,磁感应强度大小为B。带电粒子将被限制在圆环状空腔内运动。要维持带电粒子在圆环内做半径确定的圆周运动,下列说法中正确的是
[? ]
A.对于给定的加速电压,带电粒子的荷质比q/m越大,磁感应强度B越大
B.对于给定的加速电压,带电粒子的荷质比q/m越大,磁感应强度B越小
C.对于给定的带电粒子和磁感应强度B,加速电压U越大,粒子运动的周期越小
D.对于给定的带电粒子和磁感应强度B,不管加速电压U多大,粒子运动的周期都不变?
4、选择题 地球大气层外部有一层复杂的电离层,既分布有地磁场,也分布有电场,假设某时刻在该空间中有一小区域存在如图所示的电场和磁场;电场的方向在纸面内斜向左下方,磁场的方向垂直纸面向里。此时一带电宇宙粒子,恰以一定速度垂直于电场和磁场射入该区域,不计重力作用,则在该区域中,有关该带电粒子的运动情况可能的是?
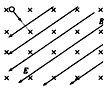
[? ]
5、选择题 建有正交坐标系O-xyz(z轴正方向竖直向上)的空间同时存在匀强电场和匀强磁场。已知电场方向沿z轴正方向场强大小为E,磁场方向沿y轴正方向磁感应强度大小为B,重力加速度为g。某质量m,电量+q的小球从原点O出发…。下列说法错误的是
[? ]
A、沿x轴正向匀速直线运动,且Eq-Bqv=mg
B、沿x轴负向匀速直线运动,且Eq=mg+Bqv
C、沿Z轴正向匀速直线运动,且Eq=Bqv+mg
D、沿y轴正向或负向匀速直线运动,且Eq=mg