时间:2017-03-05 16:45:49
1、选择题 某原子电离后其核外只有一个电子，若该电子在核的静电力作用下绕核做匀速圆周运动，那么电子运动( )
A．半径越大，加速度越大
B．半径越大，角速度越小
C．半径越小，周期越大
D．半径越小，线速度越小
参考答案：B
本题解析：根据原子核对电子的库仑力提供向心力，由牛顿第二定律得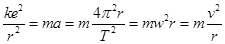
可得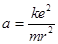
，
，
，
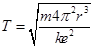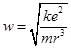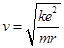.A、半径越大，加速度越小，故A错误；B、半径越大，角速度越小，故B正确；C、半径越小，周期越小，故C错误；D、半径越小，线速度越大，故D错误．故选：B．
考点：本题考查了库仑定律；匀速圆周运动．
本题难度：一般
2、简答题 如图所示，质量为m=0.1kg的小球和A、B两根细绳相连，两绳固定在细杆的A、B两点，其中A绳长LA=2m，当两绳都拉直时，A、B两绳和细杆的夹角θ1=30°，θ2=45°，g=10m/s2．求：
（1）当细杆转动的角速度ω在什么范围内，A、B两绳始终张紧？
（2）当ω=3rad/s时，A、B两绳的拉力分别为多大？
参考答案：（1）ω2=3.15（rad/s）
要使两绳都拉紧2.4 rad/s≤ω≤3.15 rad/s
（2）TA=0.27N， TB=1.09N
本题解析：（1）当B绳恰好拉直，但TB=0时，细杆的转动角速度为ω1，
有： TAcos30°=mg
解得：ω1=2．4rad/s
当A绳恰好拉直，但TA=0时，细杆的转动角速度为ω2，
有：
解得：ω2=3.15（rad/s）
要使两绳都拉紧2.4 rad/s≤ω≤3.15 rad/s
（2）当ω="3" rad/s时，两绳都紧．
?
TA=0.27N， TB=1.09N
[点评]分析两个极限（临界）状态来确定变化范围，是求解“范围”题目的基本思路和方法．
本题难度：一般
3、计算题 如图所示，电阻不计的两光滑平行金属导轨相距L=1m，PM、QN部分水平放置在绝缘桌面上，半径a=0.9m的光滑金属半圆导轨处在竖直平面内，且分别在M、N处平滑相切， PQ左端与R=2Ω的电阻连接．一质量为m=1kg、电阻r=1Ω的金属棒放在导轨上的PQ处并与两导轨始终垂直．整个装置处于磁感应强度大小B=1T、方向竖直向上的匀强磁场中，g取10m/s2．求：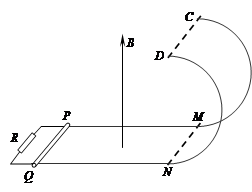
（1）若金属棒以v=3m/s速度在水平轨道上向右匀速运动，求该过程中棒受到的安培力大小；
（2）若金属棒恰好能通过轨道最高点CD处，求棒通过CD处时棒两端的电压；
（3）设LPM=LQN=3m，若金属棒从PQ处以3m/s匀速率沿着轨道运动，且棒沿半圆轨道部分运动时，回路中产生随时间按余弦规律变化的感应电流，求棒从PQ运动到CD的过程中，电路中产生的焦耳热.
参考答案：（1）1N；（2）2V（3）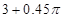
J
本题解析：⑴由
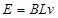得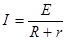 
又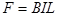
解得：F=1N
⑵在最高点CD处
得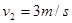
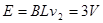
⑶在水平轨道上，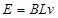 
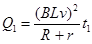=3J
在半圆轨道上，感应电动势最大值
V
=
=
J
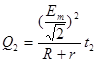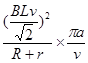J
考点：法拉第电磁感应定律；牛顿定律及能量守恒定律.
本题难度：困难
4、填空题 质量相等的两汽车以相同的速度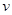
分别通过半径为
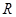的凸形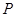路面
与凹形路面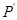
时两路面所受的压力之比为
∶
=________。
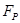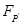参考答案：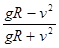
本题解析：
分析：汽车过凸形路面的最高点和通过凹形路面最低处时，重力与支持力的合力提供向心力，由牛顿第二定律列出表达式来分析判断压力与重力的关系．
解：汽车过凸形路面的最高点时，设速度为V，半径为R，由牛顿第二定律得：mg-FP=m
，
∴FP=mg-m，汽车过凹形路面的最高低时，设速度为V，半径为R，由牛顿第二定律得：FP′-mg=m，
∴FP′=mg+m，
所以凸形路面P与凹形路面P′时两路面所受的压力之比为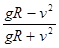
故答案为：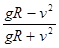
本题难度：简单
5、选择题 用长L的细线拴着一个小球，另一端固定，在竖直平面内作圆周运动，下列说法正确的是
A．小球过最高点时，速度不能超过
B．小球过最高点时速度可以为0
C．小球角速度过快时，在最低点比最高点容易断
D．小球角速度过快时，在最高点比最低点容易断
参考答案：C
本题解析：在最高点
可知速度越大绳子的拉力越大，在最低点
可知C对；ABD错；
本题难度：简单