时间:2017-03-02 10:22:53
1、计算题 如图甲所示，一个电阻值为R，匝数为n的圆形金属线圈与阻值为2R的电阻R1连接成闭合回路，线圈的半径为r1。在线圈中半径为r2的圆形区域内存在垂直于线圈平面向里的匀强磁场，磁感应强度B随时间t变化的关系图线如图乙所示。图线与横、纵轴的截距分别为t0和B0。导线的电阻不计，求0至t1时间内
(1)通过电阻R1上的电流大小和方向；
(2)通过电阻R1上的电量q及电阻R1上产生的热量。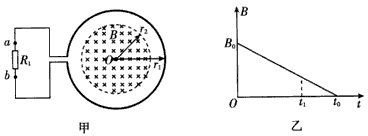
参考答案：解：(1)设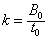
，由题图乙可知，磁感应强度B与时间t的函数关系为
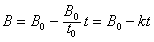①
磁场的面积及线圈内的磁通量分别为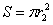
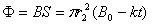?②
在0和t1时刻，单匝线圈中的磁通量分别为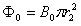
?
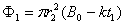
即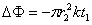
?③
在0和t1时刻，线圈中的电动势大小及电流分别为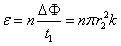
?④
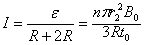?⑤
根据楞次定律判断，电阻R1上的电流方向应由b向a ⑥
(2)0至t1时间内，电阻R1上通过的电量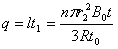
⑦
电阻R1上产生的热量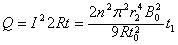
⑧
本题解析：
本题难度：困难
2、简答题 如图所示（a），在倾角为300的斜面上固定一光滑金属导轨CDEFG，OH∥CD∥FG，∠DEF=60°，CD=DE=EF=FG=AB/2=L，一根质量为m的导体棒AB在电机的牵引下，以恒定的速度v0沿OH方向从斜面底部开始运动，滑上导轨并到达斜面顶端，AB⊥OH，金属导轨的CD、FG段电阻不计，DEF段与AB棒材料、横截面积均相同，单位长度电阻为r，O是AB棒的中点，整个斜面处在垂直斜面向上磁感应强度为B的匀强磁场中．求：
（1）导体棒在导轨上滑行时电路中的电流的大小；
（2）导体棒运动到DF位置时AB两端的电压；
（3）将导体棒从低端拉到顶端电机对外做的功；
（4）若AB到顶端后，控制电机的功率，使导体棒AB沿斜面向下从静止开始做匀加速直线运动，加速度大小始终为a，一直滑到斜面底端，则此过程中电机提供的牵引力随时间如何变化？（运动过程中AB棒的合力始终沿斜面向下）．
参考答案：（1）导体棒在导轨上匀速滑行时，设AB棒等效切割长度为l，则
? 导体棒在导轨上ε=BLV0
? 回路总电阻为R总=3Lr
? 则感应电流为I=εR总
所以，I=BV03r
（2）AB棒滑到DF处时，AB两端的电压UBA=UDA+UFD+UBF
? UDA+UBF=BLv0
而UDF=2lr3lrBLv0=23BLv0
得UBA=UDA+UFD+UBF=53BLv0
（3）导体棒从低端拉到顶端电机做的功W=△EP+Q1+Q2
增加的重力势能：△EP=mg(2L+Lcos300)sin300=4+
本题解析：
本题难度：一般
3、选择题 如图所示，导线框abcd放在光滑的平行导轨上，与导轨接触良好，现使导线框abcd向右运动，G1、G2是两只电流表，则（ ）
A．G1、G2中都有电流通过
B．G1、G2中都没有电流通过
C．只有G1中有电流通过
D．只有G2中有电流通过
参考答案：导线框向右滑动时，ab边、dc边与左侧导轨构成的闭合回路磁通量增加，回路中会产生感应电流，因此有电流流过两电流表G1和G2．
故选：A．
本题解析：
本题难度：简单
4、简答题 如图，间距为L=0.9m的两金属导轨足够长，与水平面成37°角平行放置．导轨两端分别接有电阻R1和R2，且R1=R2=10Ω，导轨电阻不计．初始时S处于闭合状态，整个装置处在匀强磁场中，磁场垂直导轨平面向上．一根质量为m=750g的导体棒ab搁放在金属导轨上且始终与导轨接触良好，棒的有效电阻为r=1Ω．现释放导体棒，导体棒由静止沿导轨下滑，达到稳定状态时棒的速率为v=1m/s，此时整个电路消耗的电功率为棒的重力功率的四分之三．取g=10m/s2，已知sin37°=0.6，cos37°=0.8，求：
（1）稳定时导体棒中匀强磁场磁感应强度B；
（2）导体棒与导轨间的动摩擦因数μ；
（3）断开S后，导体棒的最终速率．
参考答案：（1）S闭合时，电路总电阻 R=R1R2R1+R2+r=6Ω，设稳定后导体棒以速率v匀速下滑．
此时棒产生的感应电动势 E=BLv
棒中电流 I=ER
电路总电功率 P总=I2R
棒的重力功率 PG=mgvsinθ
又P总═34PG
联立各式并代入数据解得：
I=
本题解析：
本题难度：一般
5、简答题 如图所示，两根足够长的光滑平行金属导轨MN、PQ间距离L=0.5m，其电阻不计，两导轨及其构成的平面与水平面成30°角．完全相同的两金属棒ab、cd分别垂直导轨放置，且都与导轨始终有良好接触．已知两金属棒质量均为m=0.02kg，电阻相等且不可忽略．整个装置处在垂直于导轨平面向上的匀强磁场中，磁感应强度B=0.2T，金属棒ab在平行于导轨向上的力F作用下，沿导轨向上匀速运动，而金属棒cd恰好能够保持静止．取g=10m/s2，求：
（1）通过金属棒cd的电流大小、方向；
（2）金属棒ab受到的力F大小；
（3）若金属棒cd的发热功率为0.1W，金属棒ab的速度．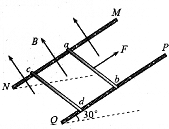
参考答案：（1）金属棒cd受到的安培力：Fcd=BIL，
金属棒cd静止处于平衡状态，由平衡条件得：Fcd=mgsin30°，
即：BIL=mgsin30°，电流为I=mgsin37°BL=0.02×10×0.50.2×0.5=1A；
由右手定则可知，通过ab棒的电流由a流向b，则金属棒cd中的电流方向由d至c；
（2）金属棒ab与cd受到的安培力大小相等：Fab=Fcd=BIL=0.2×1×0.5=0.1N
金属棒ab做匀速直线运动，处于平衡状态，由平衡条件得：
F=mgsin30°+Fab=0.02×10×0.5+0.1=0.2N；
（3）金属棒发热功率：P=I2R，
金属棒电阻：R=PI2=0.1W(1A)2=0.1Ω，
金属棒ab切割磁感线产生的 感应电动势：E=BLv，
由闭合电路欧姆定律得：I=E2R=BLv2R，
金属棒的速度：v=2IRBL=2×1A×0.1Ω0.2T×0.5m=2m/s；
答：（1）通过金属棒cd的电流大小为1A，方向：由d流向c；
（2）金属棒ab受到的力F大小为0.2N；
（3）金属棒ab的速度为2m/s．
本题解析：
本题难度：一般