时间:2020-08-15 23:38:32
1、选择题 如图所示,一偏心轮绕垂直纸面的轴O匀速转动,a和b是轮上质量相等的两个质点,则偏心轮转动过程中a、b两质点( )
A.角速度大小相同
B.线速度大小相同
C.向心加速度大小相同
D.向心力大小相同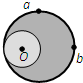
参考答案:A、偏心轮上各处角速度相等,故A正确;
B、根据v=ωr,可知半径不同点,线速度不同,故B错误;
C、根据a=ω2r可知半径不同点,向心加速度不同,故C错误;
D、根据F=mω2r可知半径不同点,向心力不同,故D错误;
故选A.
本题解析:
本题难度:简单
2、填空题 长度为L的轻质细杆,一端固定有一质量为m的小球,则小球以轻质细杆的另一端为圆心在竖直面内刚好做圆周运动时在最高点的最小速度为______,若把轻质细杆改成细绳,则小球在竖直面内刚好做圆周运动时在最高点的最小速度又为______.
参考答案:轻杆带着物体做圆周运动,只要物体能够到达最高点就可以了,所以速度可以为零,故在最高点的最小速度为零;
若把轻质细杆改成细绳,小球在最高点绳子的拉力与重力的合力提供向心力,当绳子的拉力为零时,刚好做圆周运动,速度最小,则有;
mv2L=mg
v=
本题解析:
本题难度:一般
3、简答题 在竖直转轴上有相距1m的A、B两点,A、B两点各通过1m的绳与质量为1kg小球C相连,竖直转轴转动时,小球会跟着以同样的角速度绕轴转动.求:
(1)当竖直转轴以4rad/s转动时,AC绳和BC绳的拉力大小是多少?
(2)当竖直转轴以5rad/s转动时,AC绳和BC绳的拉力大小又是多少?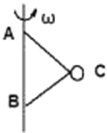
参考答案:(1)设BC绳刚好没有拉力时的角速度为ω0,此时由重力和AC绳拉力的合力提供向心力,则有:
mgtan60°=mω20Lsin60°
则得:ω0=
本题解析:
本题难度:一般
4、选择题 如图为两个内壁光滑、半径不同的半球形碗,放在不同高度的水平面上,使两碗口处于同一水平面.现将质量相同的两个带等量负电荷的小球(小球半径远小于碗的半径)分别从两个碗的边缘由静止释放,当两小球分别沿圆弧通过碗的最低点时,下列说法正确的有( )
A.当不加电场时,两小球的速度大小相等,当加竖直向上的匀强电场时,速度大小仍相等
B.当不加电场时,两小球的机械能大小相等,当加竖直向上的匀强电场时,机械能大小仍相等
C.当不加电场时,两小球对碗底的压力大小相等,若在两个碗的圆心处加一相同的点电荷,压力大小不再相等
D.当不加电场时,两小球对碗底的压力大小相等,当加竖直向上的匀强电场时,压力大小仍相等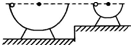
参考答案:A、B当不加电场时,小球从图示位置到最低点的过程中机械能守恒,取初位置为零势能面,则有
? mgR=12mv2,得v=
本题解析:
本题难度:简单
5、选择题 如图所示,固定的锥形漏斗内壁是光滑的,内壁上有两个质量相等的小球A和B,在各自不同的水平面做匀速圆周运动,以下说法正确的是( )
A.A的线速度大于B的线速度
B.A的角速度大于B的角速度
C.A的加速度大小等于B的加速度大小
D.A对漏斗内壁的压力小于B对漏斗内壁压力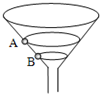
参考答案:物体受力如图:将FN沿水平和竖直方向分解得:FNcosθ=ma ①,FNsinθ=mg ②.
由②可知支持力相等,则A、B对内壁的压力大小相等.
根据牛顿第二定律,合外力提供向心力,合外力相等,则向心力相等.由①②可得:mgcotθ=ma=mv2r=mω2R.可知半径大的线速度大,角速度小.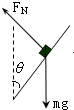
则A的线速度大于B的线速度,A的角速度小于B的角速度,A、B的向心加速度相等.故A、C正确,B、D错误.
故选AC.
本题解析:
本题难度:简单