时间:2020-08-15 22:46:59
1、选择题 如图所示,匀强电场水平向左,带正电物体沿绝缘、粗糙水平板向右运动,经A点时动能为100J,到B点时动能减少到80J.减少的动能中有12J转化为电势能,则它再经过B点时,动能大小是(?) 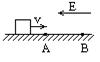
A.4J
B.16J
C.32J
D.64J
参考答案:B
本题解析:
试题分析: 设物体向右运动到C点静止,然后返回,AB间距离为x1,BC间距离为x2,
由A到B过程中,则由动能定理得:(f+qE)x1=(80-100)J
电场力做功与电势能的关系:qEx1=12J,解得:qE=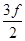
由B到C过程中,则由动能定理得:-(f+qE)x2=-80J
解得fx2=32J
由B到C再返回B点过程中,则由动能定理得:-2 fx2=Ek-80;解得:Ek=16J故选项B正确。
本题难度:一般
2、选择题 如图所示,质量为m的物体从斜面上的A处由静止滑下,停在水平面上的B点(斜面与水平面通过一小段与它们相切的圆弧连接),量得A、B两点间的水平距离和B、C间距离均为s,物体与斜面及水平面的动摩擦因数均为μ,如果用与轨道平行的力F把物体从C处拉回A处,则力F做的功至少为( )
A.μmgs
B.2μmgs
C.3μmgs
D.4μmgs
参考答案:对A到C运动的过程,运用动能定理,有:mgh-μmgcosθs′-μmgs″=0,即mgh-μmg?s=0.得出,mgh=μmgs.
对C到A运用动能定理得,WF-mgh-Wf=0,所以WF=mgh+Wf=μmgs+2μmgs=3μmgs.故C正确,A、B、D错误.
故选C.
本题解析:
本题难度:一般
3、计算题 如图所示,有一半径为R的半圆形圆柱面MPQ,质量为2m的A球与质量为m的B球,用轻质绳连接后挂在圆柱面边缘.现将A球从边缘M点由静止释放,若不计一切摩擦。
求:(1)A球沿圆柱面滑到最低点P点的过程中,A、B构成的系统机械能是否守恒?
(2)A球沿圆柱面滑到最低点P时,A、B的速度之比;
(3)A球沿圆柱面滑到最低点P时的速度大小.
参考答案:(1)守恒 ?(2)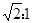 ? (3)
? (3)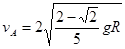
本题解析:(1)A球沿圆柱面滑到最低点P点的过程中,A、B构成的系统,只有重力对AB做功,所以机械能守恒?(3‘)
(2)由图可知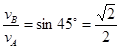 ,所以
,所以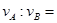
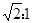 (3‘)
(3‘)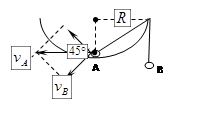
(3)对AB系统在运动过程中由动能定理得: ?(3‘)
?(3‘)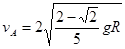 ?(3‘)
?(3‘)
本题难度:一般
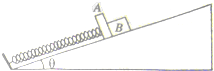
4、选择题 如图所示,在倾角为θ的斜面上,轻质弹簧一与斜面底端固定,另一端与质量为M的平板A连接,一个质量为m的物体B靠在平板的右测,A、B与斜面的动摩擦因数均为μ.开始时用手按住物体B使弹簧处于压缩状态,现放手,使A和B一起沿斜面向上运动距离L时,A和B达到最大速度v.则以下说法正确的是( )
A.A和B达到最大速度v时,弹簧是自然长度
B.若运动过程中A和B能够分离,则A和B恰好分离时,二者加速度大小均为g(sinθ+μcosθ)
C.从释放到A和B达到最大速度v的过程中.弹簧对A所做的功等于
| 1 2 |
| 1 2 |
参考答案:A、A和B达到最大速度v时,A和B的加速度应该为零.
对AB整体:由平衡条件知
kx-(m+M)gsinθ-μ(m+M)gcosθ=0,
所以此时弹簧处于压缩状态.故A错误.
B、A和B恰好分离时,AB间的弹力为0,对B受力分析:由牛顿第二定律知,
沿斜面方向,mgsinθ+μmgcosθ=ma,
得a=gsinθ+μgcosθ,
由牛顿第二定律知,A,B的加速度相同,故B正确.
C、从释放到A和B达到最大速度v的过程中,对于AB整体,根据动能定理得
-(m+M)gLsinθ-μ(m+M)gcosθ?L+W弹=12(m+M)v2
弹簧对A所做的功W弹=12(m+M)v2+(m+M)gLsinθ+μ(m+M)gcosθ?L,故C错误.
D、从释放到A和B达到最大速度v的过程中,对于B,根据动能定理得
B受到的合力对它做的功W合=△Ek=12mv2,故D正确.
故选:BD.
本题解析:
本题难度:简单
5、简答题 如图所示,半径为R=0.45m的光滑的1/4圆弧轨道AB与粗糙平面BC相连,质量m=2kg的物块由静止开始从A点滑下经B点进入粗糙水平面,受到的阻力是物重的0.2倍.试求:
(1)物块经B点时的速度大小v;
(2)物体沿水平面运动过程中克服摩擦力做多少功?
(3)物块经B点后在BC平面滑行的最大距离s.
参考答案:(1)对AB段运用动能定理得,mgR=12mvB2,解得vB=
本题解析:
本题难度:一般