时间:2020-08-09 23:49:35
1、简答题 柴油打桩机的重锤由气缸、活塞等若干部件组成，气缸与活塞间有柴油与空气的混合物．在重锤与桩碰撞的过程中，通过压缩使混合物燃烧，产生高温高压气体，从而使桩向下运动，锤向上运动．现把柴油打桩机和打桩过程简化如下：
柴油打桩机重锤的质量为m，锤在桩帽以上高度为h处（如图1）从静止开始沿竖直轨道自由落下，打在质量为M（包括桩帽）的钢筋混凝土桩子上．同时，柴油燃烧，产生猛烈推力，锤和桩分离，这一过程的时间极短．随后，桩在泥土中向下移动一距离l．已知锤反跳后到达最高点时，锤与已停下的桩幅之间的距离也为h（如图2）．已知m=1.0×103kg，M=2.0×103kg，h=2.0m，l=0.20m，重力加速度g=10m/s2，混合物的质量不计．设桩向下移动的过程中泥土对桩的作用力F是恒力，求此力的大小．
参考答案：锤自由下落，碰桩前速度v1向下，v1=
本题解析：
本题难度：一般
2、选择题 如图所示，子弹水平射入放在光滑水平地面上静止的木块，子弹未穿透木块，此过程产生的内能为6J，那么此过程木块动能可能增加了（ ）
A．12J
B．16J
C．4J
D．6J
参考答案：设子弹的初速度为V，射入木块后子弹与木块共同的速度为v，木块的质量为M，子弹的质量为m．
根据动量守恒定律得：mV=（M+m）v
得，v=mVM+m
木块获得的动能为△Ek=12Mv2
系统产生的内能为Q=12mV2-12(M+m)v2=MmV22(M+m)=12Mv2?mM+m＜12Mv2=△Ek
则得到△Ek＞Q=6J
故选AB
本题解析：
本题难度：简单
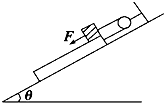
3、选择题 如图所示，在倾角为θ的光滑斜面上，一根细绳通过定滑轮分别与木板、小滑块（可视为质点）相连，小滑块质量为m，木板质量为M，木板长为L，小滑块与木板间的动摩擦因数为μ，开始时小滑块静止在木板的上端，现用与斜面平行的拉力F将小滑块缓慢拉至木板的下端，则在此过程中（ ）
A．拉力F的大小为mgμcosθ+（M-m）gsinθ
B．拉力F的大小为2mgμcosθ+（M-m）gsinθ
C．拉力F做的功为mgμLcosθ+（M-m）gLsinθ
D．拉力F做的功为mgμLcosθ+
| L 2 |
参考答案：
A、B对木板：设细绳的拉力大小为T．根据平衡条件得：T=Mgsinθ+μmgcosθ
? 对小滑块：由平衡条件得：F+mgcosθ=T+μmgcosθ
联立上两式得：F=2mgμcosθ+（M-m）gsinθ? 故A错误，B正确．
C、DF是恒力，将小滑块缓慢拉至木板的下端过程中，滑块相对地的位移大小为L2，则拉力F做的功为W=F?L2=mgμLcosθ+L2(M-m)gsinθ．故C错误，D正确．
故选BD
本题解析：
本题难度：简单
4、计算题 （18分）如图所示,固定的凹槽水平表面光滑,其内放置U形滑板N,滑板两端为半径R="0.45" m
的1/4圆弧面,A和D分别是圆弧的端点,BC段表面粗糙,其余段表面光滑,小滑块P1和P2的质量均为m,滑板的质量M=4m.P1和P2与BC面的动摩擦因数分别为μ1=0.10和μ2=0.40,最大静摩擦力近似等于滑动摩擦力,开始时滑板紧靠槽的左端,P2静止在粗糙面的B点。P1以v0="4.0" m/s的初速度从A点沿弧面自由滑下,与P2发生弹性碰撞后,P1停在粗糙面B点上,当P2滑到C点时,滑板恰好与槽的右端碰撞并与槽牢固粘连,P2继续滑动,到达D点时速度为零,P1与P2可视为质点,取g="10" m/s2。问：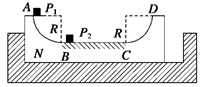
（1）P2在BC段向右滑动时,滑板的加速度为多大？
（2）BC长度为多少？N、P1和P2最终静止后,P1与P2间的距离为多少？
参考答案：（1）
（2）1.9m? 0.695m
本题解析： (1) P2在BC段向右滑动时，P1停在粗糙面B点上。将N、P1看作整体，根据牛顿第二定律得：
?①
?②
(2)设P1到达B点的速度为v，P1从A点到达B点的过程中，根据动能定理有：
?③
代入数据得
?④
因P1、P2质量相等且发生弹性碰撞，所以碰后P1、P2交换速度，即碰后P2在B点的速度为：
?⑤
设P2在C点的速度为
，P2从C点到D点过程中根据动能定理得：
?⑥
代入数据得
?⑦
P2从B点到C点的过程中，N、P1、P2作为一个系统所受合外力为零，系统动量守恒，设P2到达C点时N和P1的共同速度为
.根据动量守恒定律得：
?⑧
v′为滑板与槽的右端粘连前滑板和P1的共同速度．对P2从B点到C点相对地面位移为
由动能定理
?⑨
P1 和N作为一个整体，相对地面位移为
，根据动能定理则有
?⑩
联立⑧⑨⑩得BC长度
?
滑板与槽粘连后，P1在BC上移动的距离为
，根据动能定理
?
P2在D点滑下后，在BC上移动的距离
，根据动能定理有
?
联立得系统完全静止时P1与P2的间距
?
⑥⑧⑨⑩各2分，其余各1分
本题难度：一般
5、简答题 如图所示，有一质量为m的物块静止在水平桌面左端，长为L的细线竖直悬挂一个质量为2m的小球，小球刚好与物块接触．现保持细线绷直，把小球拉向左上方使细线与竖直方向成60°夹角，无初速释放，小球运动到最低点时恰与物块正碰，碰后小球继续向右摆动，上升的最大高度为
| L 8 |
参考答案：设碰前小球速度为v，碰后小球速度为v1，物块速度为v2．
对小球下摆过程分析，根据机械能守恒：
? 2mgL（1-cos60°）=12?2mv2 ①
解得：v=
本题解析：
本题难度：一般