时间:2020-08-09 23:37:29
1、选择题 在一个边界为等边三角形的区域内，存在一个方向垂直于纸面向内的匀强磁场，在磁场边界上的P点处有一个粒子源，发出比荷相同的三个粒子a、b、c（不计重力）沿同一方向进入磁场，三个粒子通过磁场的轨迹如图所示，用ta、tb、tc分别表示a、b、c通过磁场的时间；用ra、rb、rc分别表示a、b、c在磁场中的运动半径，则下列判断正确的是
A．ta=tb＞tc
B．tc＞tb＞ta
C．rc＞rb＞ra
D．rb＞ra＞rc
参考答案：AC
本题解析：出射点为a、b的粒子在磁场中转过的圆心角相同，运动时间
，因为粒子比荷相同，所以运动时间相同，即ta=tb，根据几何关系可知从c点射出的粒子转过的圆心角较小，则运动时间也较短，所以ta=tb＞tc，故A正确B错误
根据几何关系可知，出射点为a的粒子在磁场中运动半径，小于出射点为b的粒子在磁场中的运动半径，出射点为b的粒子在磁场中的运动半径，小于出射点为c的粒子在磁场中的运动半径，即. rc＞rb＞ra，故C正确D错误
故选AC
本题难度：一般
2、选择题 如图所示圆形区域内有垂直于纸面的匀强磁场，三个质量和电荷量都相同的带电粒子a、b、c，以不同的速率沿着AO方向对准圆心O射入磁场，其运动轨迹如图所示。若带电粒子只受磁场力的作用，则下列说法正确的是( )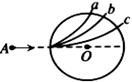
A．a粒子速率最大
B．c粒子在磁场中运动的时间最长
C．c粒子速率最大
D．它们做圆周运动的周期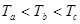
参考答案：C
本题解析：由带电粒子在磁场中的偏转半径公式R=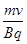
，因为质量m、q、B都相等，所以半径越大的，速度也越大，因为c的半径最大，故它的速度最大，C正确；因为粒子的磁场中做圆周运动的周期为T=
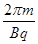，大小是不变的，故D错误；而c粒子在磁场中的偏角最小，故它在磁场中的运动时间最短，B错误。
考点：粒子在磁场中的偏转。
本题难度：一般
3、计算题 如图所示，水平地面上方分布着水平向右的匀强电场，场强大小为E0，一个弯成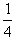
圆周的环状绝缘硬质细管AB竖直固定在匀强电场中。环的半径R=0.30m，离水平面地面的距离为h=5.0m，一带正电的小球从管的上端口A处静止释放，小球大小略小于管的直径，它与管间摩擦不计，小球在电场中受到的电场力大小为重力的一半。（g=10m/s2）求：
（1）小球运动到管口B时的速度大小；
（2）若使带电小球离开环B点瞬间，突然撤去匀强电场，为了使带电小球向右做匀速直线运动，可以加垂直纸面方向的匀强磁场，试求磁场的方向以及磁感应强度大小和原匀强电场强度E的比。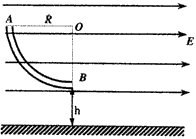 
参考答案：解：（1）在小球A运动到B的过程中，只有重力和电场力做功。由动能定理有：
?①
由题意可知
②
联立①②式解得：
③
代入数据可得：
④
（2）为了满足题意，只有加方向为垂直纸面向里的匀强磁场时才行。当洛仑兹力和重力平衡时，带电小球才可能做匀速直线运动。故
? ⑤
由于
?⑥
联立④⑤⑥式得
本题解析：
本题难度：困难
4、计算题 （10分）（创编）如图所示，质量为m、电量为-q的小球，可在半径为R的固定半圆形光滑的绝缘轨道两端点M，N之间来回滚动，磁场磁感强度B垂直于轨道平面，小球在M、N处速度为零。若小球在最低点的最小压力为零，那么磁感强度B为多大？小球对轨道最低点的最大压力为多大？
（已知重力加速度为g）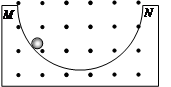
参考答案：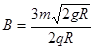
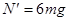
本题解析：
洛伦兹力不改变速度的大小，小球向左和向右通过轨道的最低点速度大小是一样的，但洛伦兹力的方向相反。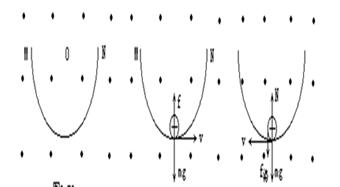
小球由M处静止滑下，到最低点的速度为v，由动能定理（或机械能守恒定律）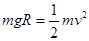
①
在最低点处，由向心力公式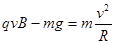 
②
联立①②式得：。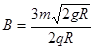
小球从N点静止滑下，到最低点对轨道压力最大，由动能定理（或机械能守恒定律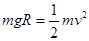） ③
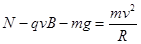④
由③、④式解得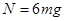 
。 由牛顿第三定律。
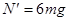考点：带电粒子在匀强磁场中的运动；圆周运动；向心力。
本题难度：一般
5、简答题 如图所示，坐标系xOy位于竖直平面内，空间中有沿水平方向、垂直纸而向外的匀强磁场，磁感应强度大小为B，在x＞0的空间内有沿x轴正方向的匀强电场，电场强度大小为E．一带正电荷的小球从图中x轴上的M点沿着与水平方向成θ=30°角的斜向下的直线做匀速运动，进过y轴上的N点进入x＜0的区域．要使小球进入x＜0的区域后能在竖直面内做匀速圆周运动，需要在x＜0的区域内另加一匀强电场．已知带电小球做圆周运动时通过y轴上的P点（P点未标出），重力加速度为g，求：
（1）小球运动的速度大小；
（2）在x＜0的区域内所加匀强电场的电场强度的大小和方向；
（3）N点与P点间的距离．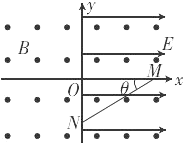
参考答案：（1）对小球在MN段的运动进行受力分析（如右图所示），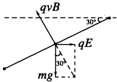
因小球做匀速直线运动，所以有：
qvBsin30°=qE
解得：小球运动的速度大小为 v=2EB．
（2）在x＜0的区域内，设所加的电场强度为E′，则由运动情况分析知，小球受的重力mg必与电场力qE′是一对平衡力，即有：
qE′=mg
又 mgtan30°=qE
故可得：E′=
本题解析：
本题难度：一般