时间:2020-08-09 23:00:53
1、填空题 如图所示,电子射线管(A为其阴极),放在蹄形磁铁的N、S两极间,射线管的阴极(A)接直流高压电源的______极.(正、负)?此时,荧光屏上的电子束运动径迹将______偏转.(填“向上”、“向下”或“不”).
2、选择题 如图所示,虚线框内为一长方形区域,内有匀强磁场,一束质子以不同的速度从O点垂直磁场方向射入后,分别从a、b、c、d四点射出.比较它们在磁场的运动时间是(?)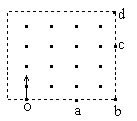
A.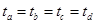
B.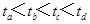
C.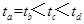
D.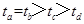
3、选择题 1998年6月3日,美国发射的航天飞机,其中一个关键部件是由中国科学院设计制造的直径为120mm、高为80 mm、中心磁感应强度为0.134T的永磁体,它的主要使命是要探测宇宙空间中可能存在的反物质,特别是宇宙中反氦原子的原子核,若图中的α磁谱仪中的四条径迹分别为质子、反质子、α粒子、反氦原子核经粒子速度选择器后,再进入匀强磁场形成的径迹,则其中反氦原子核的径迹是?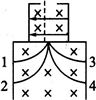
[? ]
A.1?
B.2?
C.3?
D.4
4、选择题 如图,虚线MN上方存在方向垂直纸面向里的匀强磁场B1,带电粒子从边界MN上的A点以速度vo垂直磁场方向射人磁场,经磁场偏转后从边界MN上的B点射出。若在粒子经过的区域PQ上方再叠加方向垂直纸面向里的匀强磁场B2,让该粒子仍以速度v0从A处沿原方向射人磁场,经磁场偏转后从边界MN上的B"点射出(图中未标出),不计粒子的重力。下列关于粒子的说法正确的是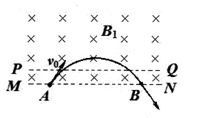
A.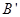 点在B点的右侧
点在B点的右侧
B.从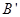 点射出的速度大于从B点射出的速度
点射出的速度大于从B点射出的速度
C.从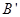 点射出的速度方向平行于从B点射出的速度方向
点射出的速度方向平行于从B点射出的速度方向
D.从A到B"的时间等于从A到B的时间
5、填空题 电子枪射出的电子速度是107m/s,垂直进入磁感应强度为0.3T的磁场,此时电子受到的洛仑兹力大小是______N,洛仑兹力的方向与电子速度方向______.(元电荷e=1.6×10-19C)