时间:2020-08-09 22:55:18
1、计算题 如图一个质量为m、电量为e的静止质子,经电压为U的电场加速后,射入与其运动方向一致的磁感应强度为B的匀强磁场MN区域内。在MN内有n块互成直角、长为L的硬质塑料板(不导电,宽度很窄,厚度不计)。
(1)求质子进入磁场时的速度v0;
(2)若质子进入磁场后与每块塑料板碰撞后均没有能量损失且满足反射原理,求质子穿过磁场区域所需的时间t。 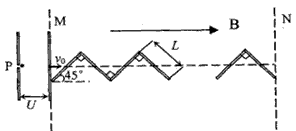
参考答案:解:(1)根据动能定理: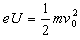 ,得
,得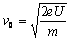
(2)质子打到第一块板上后速度与原速度方向垂直,由于没有能量损失,仍以大小为v0的速度垂直磁场方向,以半径R在垂直于磁场的平面内做匀速圆周运动,转动一周后打到第一块板的下部。由于不计板的厚度,所以质子从第一次打到板后到第二次打到板运动时间为质子磁偏转周期T
根据牛二定律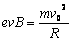 和运动学
和运动学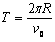 ,得
,得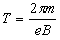
质子在磁场中共碰到n块板,做圆周运动所需要时间为t2=nT
质子进入磁场中,在v0方向的总位移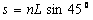
时间为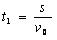
则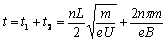
本题解析:
本题难度:困难
2、简答题 在地面附近的真空中,存在着竖直向上的匀强电场和垂直电场方向水平向里的匀强磁场,如图甲所示。磁场随时间变化情况如图乙所示.该区域中有一条水平直线MN,D是MN上的一点.在t=O时刻,有一个质量为m、电荷量为+q的小球(可看作质点),从M点开始沿着水平直线以速度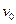 做匀速直线运动,
做匀速直线运动,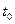 时刻恰好到达N点.经观测发现,小球在t=2
时刻恰好到达N点.经观测发现,小球在t=2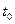 至t=3
至t=3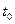 时间内的某一时刻,又竖直向下经过直线MN上的D点,并且以后小球多次水平向右或竖直向下经过D点.求:
时间内的某一时刻,又竖直向下经过直线MN上的D点,并且以后小球多次水平向右或竖直向下经过D点.求:
(1)电场强度E的大小;
(2)小球从M点开始运动到第二次经过D点所用的时间;
(3)小球运动的周期,并画出运动轨迹(只画一个周期).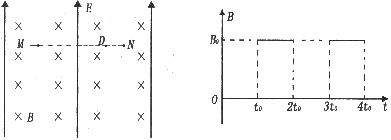
甲?乙
参考答案:(1)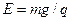 (2)
(2)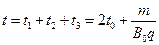 (3)
(3)
本题解析:(1)小球从M到N有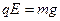
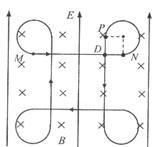
解得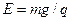
(2)小球从M点到达N点所用时间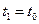
小球从N点经过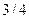 个圆周,到达P点,所以
个圆周,到达P点,所以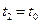
小球从P点到D点的位移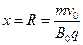
小球从P点到D点的时间为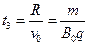
所以:时间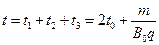
(或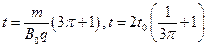 )
)
(3)小球运动一个周期的轨迹如图所示
小球的运动周期为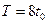 ?(或
?(或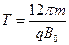 )
)
本题难度:一般
3、计算题 如图甲,在x>0的空间中存在沿y轴负方向的匀强电场和垂直于xoy平面向里的匀强磁场,电场强度大小为E,磁感应强度大小为B。一质量为q(q>0)的粒子从坐标原点O处,以初速度v0沿x轴正方向射入,粒子的运动轨迹见图甲,不计粒子的质量。
(1)求该粒子运动到y=h时的速度大小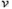 ;
;
(2)求粒子在y方向上的最大位移;
(3)证明粒子在y方向做的是简谐振动并求振动方程。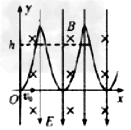
参考答案:解:(1)动能定理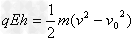 ?
?
解得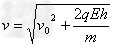 ?
?
(2)粒子的两个分运动:水平方向匀速直线运动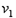 ?
?
竖直方向匀速圆周运动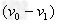 ?
?
则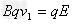 ?
? 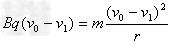 ?
?
解得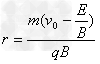
则y方向上最大位移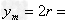
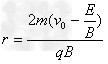 ?
?
(3)由图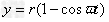
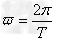 ?
? 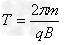 ?
?
解得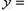
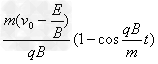
本题解析:
本题难度:困难
4、计算题 如图所示,光滑绝缘水平面的上方空间被竖直的分界面MN分隔成两部分,左侧空间存在一水平向右的匀强电场,场强大小?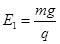 右侧空间有一长为R=0.8m的绝缘轻绳,绳的一端固定于O点,另一端拴一个质量m2=m的不带电的小球B在竖直平面内做顺时针方向的圆周运动,运动到最低点时速度大小vB=8m/s,小球B在最低点时与地面接触但没有弹力. 在MN左侧空间中有一个质量为m1=m的带正电的物体A,电荷量大小为q,在水平面上与MN界面水平间距为L处由静止释放,恰好与运动到最低点处的B发生正碰,并瞬间粘合成一个整体C,碰后瞬间在MN的右侧空间立即加上一竖直向上的匀强电场,场强大小E2=3E1(g=10m/s2)
右侧空间有一长为R=0.8m的绝缘轻绳,绳的一端固定于O点,另一端拴一个质量m2=m的不带电的小球B在竖直平面内做顺时针方向的圆周运动,运动到最低点时速度大小vB=8m/s,小球B在最低点时与地面接触但没有弹力. 在MN左侧空间中有一个质量为m1=m的带正电的物体A,电荷量大小为q,在水平面上与MN界面水平间距为L处由静止释放,恰好与运动到最低点处的B发生正碰,并瞬间粘合成一个整体C,碰后瞬间在MN的右侧空间立即加上一竖直向上的匀强电场,场强大小E2=3E1(g=10m/s2)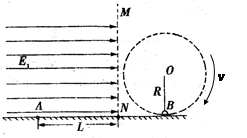
(1)如果L=0.2m,求出整体C运动到最高点时的瞬时速度大小,及此时绳的拉力是物体重力的多少倍?
(2)当L满足什么条件时,整体C可以在竖直面内做一个完整的圆周运动?
参考答案:(1)T="7.25" mg?(2)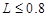 m或
m或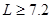 m,整体C在竖直面内做一个完整的圆周运动.
m,整体C在竖直面内做一个完整的圆周运动.
本题解析:(1)物A与B碰前速度为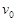 ,有动能定理:
,有动能定理: ?∴
?∴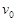 ="2" m/s
="2" m/s
A、B作用动量守恒:
∴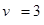 m/s,即C顺时针转动
m/s,即C顺时针转动
C有最底点→最高点速度为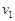 有动能定理:
有动能定理: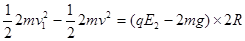
∴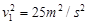 ?即
?即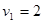 m/s?…………5分
m/s?…………5分
在最高点处: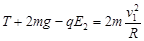 ∴T="7.25" mg?…………5分
∴T="7.25" mg?…………5分
(2)合成C后:∵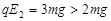 ,C的合力向上,
,C的合力向上,
即C在最底处有最小速度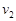 :
: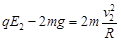 ∴
∴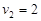 m/s
m/s
令C顺时针: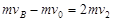 ,∴
,∴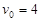 m/s,则
m/s,则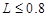 m?…………5分
m?…………5分
令C逆时针: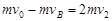 ,∴
,∴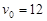 m/s,则
m/s,则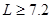 m?…………5分
m?…………5分
即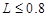 m或
m或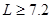 m,整体C在竖直面内做一个完整的圆周运动.
m,整体C在竖直面内做一个完整的圆周运动.
本题难度:一般
5、计算题 如图所示,在xOy平面内有一范围足够大的匀强电场,电场强度大小为E,电场方向在图中未画出.在y≤l的区域内有磁感应强度为B的匀强磁场,磁场方向垂直于xOy平面向里.一电荷量为+q、质量为m的粒子,从O点由静止释放,运动到磁场边界P点时的速度刚好为零,P点坐标为(l,l),不计粒子所受重力. 
(1)求从O到P的过程中电场力对带电粒子做的功,并判断匀强电场的方向.
(2)若该粒子在O点以沿OP方向、大小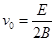 的初速度开始运动,并从P点离开磁场,此过程中运动到离过OP的直线最远位置时的加速度大小
的初速度开始运动,并从P点离开磁场,此过程中运动到离过OP的直线最远位置时的加速度大小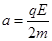 ,则此点离OP直线的距离是多少?
,则此点离OP直线的距离是多少?
(3)若有另一电荷量为-q、质量为m的粒子能从O点匀速穿出磁场,设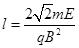 ,求该粒子离开磁场后到达y轴时的位置坐标.
,求该粒子离开磁场后到达y轴时的位置坐标.
参考答案:(1)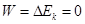 ;电场方向应为斜向右下与x轴正方向成45°(2)
;电场方向应为斜向右下与x轴正方向成45°(2)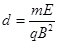 (3)
(3)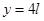
本题解析:(1)根据动能定理,从O到P的过程中电场力对带电粒子做的功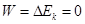 ?
?
所以直线OP是等势线,带电粒子能在复合场中运动到P点,则电场方向应为斜向右下与x轴正方向成45°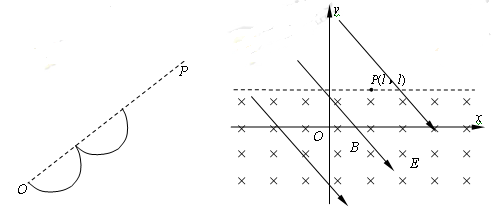
(2)磁场中运动到离直线OP最远位置时,速度方向平行于OP.洛伦兹力方向垂直于OP,设此位置粒子速度为v、离OP直线的距离为d,则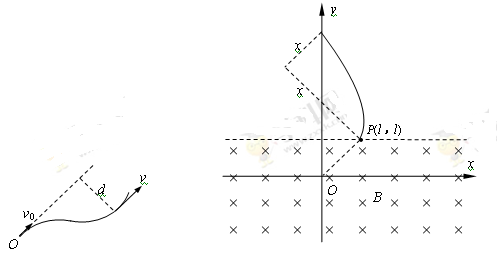
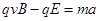 ?
?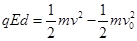 ?
?
解得?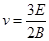 ?
?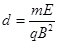
(3)设粒子做匀速直线运动速度为v1,则?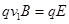
设粒子离开P点后在电场中做类平抛运动的加速度为a′,设从P点运动到y轴的过程中,粒子在OP方向的位移大小为x,则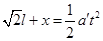
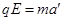 ?
?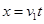 ?
?
解得?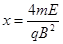 ?
?
粒子通过y轴时的纵坐标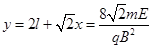
(或写成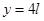 )
)
本题难度:一般