时间:2020-08-09 22:22:37
1、选择题 如图所示,一圆盘可绕通过圆盘中心O且垂直于盘面的竖直轴转动.在圆盘上放置一木块.当圆盘匀速转动时,木块随圆盘一起运动.那么( )
A.木块受到圆盘对它的摩擦力,方向背离圆盘中心
B.木块受到圆盘对它的摩擦力,方向指向圆盘中心
C.因为木块随圆盘一起运动,所以木块受到圆盘对它的摩擦力,方向与木块的运动方向相同
D.因为摩擦力总是阻碍物体运动,所以木块所受圆盘对它的摩擦力的方向与木块的运动方向相反
参考答案:对木块受力分析可知,木块受到重力、支持力和摩擦力的作用,
重力是竖直向下的,支持力是竖直向上的,重力和支持力都在竖直方向上,这两个力为平衡力,
只有摩擦力作为了物体做圆周运动的向心力,所以摩擦力的方向应该是指向圆心的,所以B正确.
故选B.
本题解析:
本题难度:一般
2、选择题 质量为m的小球在竖直平面内的圆形轨道的内侧运动,经过最高点而不脱离轨道的最小速度是v,则当小球以2v的速度经过最高点时,对轨道压力的大小是
[? ]
A.0
B.mg
C.3mg
D.5mg
参考答案:C
本题解析:
本题难度:一般
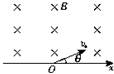
3、简答题 如图所示,x轴上方有垂直纸面向里的匀强磁场.有两个质量相同,电荷量也相同的带正、负电的离子(不计重力),以相同速度从O点射入磁场中,射入方向与x轴均夹30°角.求正、负离子在磁场中运动半径比
| r正 r负 |
| t正 t负 |
参考答案:(1)由于离子所需向心力由洛伦兹力提供,则: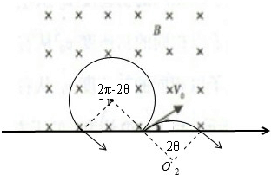
? qvB=mv2r? ①
故:r=mvqB? ②
由于正负离子的速度、带电量是相同的,因此:r正r负=11
(2)如图所示,由洛伦兹力提供向心力得:qvB=m(2πT)2r?③
由②③式得:T=2πmqB
由于正负离子的质量和带电量都相同,因此周期也相同.
而由图可知:轨迹圆心角分别为Φ正=2π-2θ=5π3,Φ负=2θ=π3
故:t正=Φ?正2πT,t负=Φ?负2πT
因此:t正t负=Φ正Φ负=51
答:正、负离子在磁场中运动半径比r正r负是11,时间比t正t负是51.
本题解析:
本题难度:一般
4、选择题 如图所示,内壁光滑的圆锥筒的轴线垂直于水平面,圆锥筒固定不动,两个质量相同的小球A和B紧贴着内壁分别在图中所示的水平面内做匀速圆周运( )
A.球A的角速度一定大于球B的角速度
B.球A的线速度一定大于球B的线速度
C.球A的运动周期一定小于球B的运动周期
D.球A对筒壁的压力一定大于球B对筒壁的压力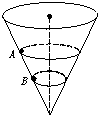
参考答案:A、对小球受力分析,受重力和支持力,如图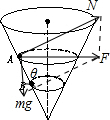
根据牛顿第二定律,有
F=mgtanθ=mv2r解得
v=
本题解析:
本题难度:一般
5、选择题 如图所示,将悬线拉至水平位置无初速释放,当小球到达最低点时,细线被一与悬点同一竖直线上的小钉B挡住,比较悬线被小钉子挡住的前后瞬间,①小球的机械能减小?②小球的动能减小③悬线的张力变大?④小球的向心加速度变大,以上说法正确的是
[? ]
A.①②
B.③④
C.②③
D. ①④
①④
参考答案:B
本题解析:
本题难度:一般