时间:2019-12-13 02:46:53
1、计算题 某一长直的赛道上，有一辆F1赛车前方200m处有一安全车正以10m/s的速度匀速前进，这时赛车从静止出发以2m/s2的加速度追赶。试求：
（1）赛车出发3s末的瞬时速度大小；
（2）赛车何时追上安全车？
（3）赛车追上安全车之前何时与安全车距离最远？
参考答案：（1）6 m/s
（2）20 s
（3）5 s
本题解析：
本题难度：困难
2、计算题 某同学的家住在一座30层的高楼内，他每天乘电梯上楼，经过多次仔细观察和反复测量，他发现电梯启动后向上运动的速度符合如下图所示的规律，他就根据这一特点在电梯内用台秤、重物和秒表测量这一楼房的高度。他将台秤放在电梯内，将重物放在台秤的托盘，电梯从第一层开始启动，经过不间断地运行，最后停在第30楼。他测得在第9.5s时台秤的示数为60N，g=10m/s2。求：
（1）电梯启动后在上升过程中台秤的最大示数；
（2）该幢楼房每一层的平均高度（结果保留3位有效数字）。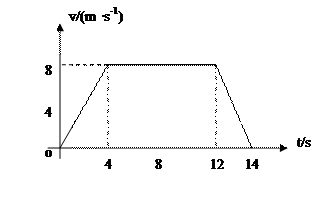
参考答案：（1）解：依据v-t图可知，当t=9.5s时电梯匀速运动，则重物的重力是60N，在0~4s内台秤的示数最大(1分);a= (vt-v0)/t(1分)；根据牛顿第二定律，有F-mg=ma(2分);又根据牛顿第三定律F’=F;
解得F’=72N(1分)，即台秤的最大示数为72N.
（2）(5分)高度s=“面积”=88m(2分); 平均每层高度h1=s/29(2分);
h=3.03m
本题解析：略
本题难度：简单
3、计算题 在一条平直的公路上，乙车以v乙＝10m/s的速度匀速行驶，甲车在乙车的后面作初速度为v甲＝15m/s，加速度大小为a＝0.5m/s2的匀减速运动，则两车初始距离L满足什么条件时可以使（设两车相遇时互不影响各自的运动）：
（1）两车不相遇；
（2）两车只相遇一次；
（3）两车能相遇两次。
参考答案：解：设两车速度相等经历的时间为t0，此时两车间的距离最小，设为L0。甲车恰能追及乙车就是在此时刻，应有 
其中
解得：L0＝25m ? 
（1）若L＞L0＝25m，则两车速度相等时甲车也未追及乙车，以后间距会逐渐增大，两车不相遇；
（2）若L＝L0＝25m，则两车速度相等时甲车恰好追上乙车，以后间距会逐渐增大，两车只相遇一次；
（3）若L＜L0＝25m，在两车速度相等前，甲车追上并超过乙车，甲车运动至乙车前面，当两车的速度相等时两车间的距离最大。此后甲车的速度小于乙车的速度，两者间的距离又逐渐减小，乙车追上并超过甲车，两车再次相遇。乙车超过甲车后两者间的距离逐渐增大，不会再相遇，即两车能相遇两次。
本题解析：
本题难度：困难
4、选择题 一物体做匀变速直线运动，某时刻速度的大小为3m/s，在1s后其速度大小变为9m/s，在这1s内该物体的(? )
A．位移的大小可能等于6m
B．位移的大小一定等于3m
C．加速度的大小可能等于6m/s2
D．加速度的大小可能等于3m/s2
参考答案：AC
本题解析：当初速度与末速度同向时，平均速度为
，1s内位移为
，所以A正确；B错误；加速度
，所以C正确；若初、末速度反向，则加速度
，所以D错误。
本题难度：简单
5、计算题 一物体从斜面顶端由静止开始匀加速下滑到斜面底端，最初3s内经过的路程为s1，最后3s内经过的路程为s2，已知s2 －s1 = 1.2m，s1：s2 = 3 ：7，求：
（1）加速度为多大？
（2）滑到斜面底端时速度？
（3）斜面长度？
参考答案：解：（1）由已知条件得：S1 = 0.9m，S2 = 2.1m
? 由公式S1 = at2/2 得加速度a = 0.2m/s2
（2）由运动可逆性，在最后3s内，未速度为V，有：S2 = Vt－at2/2
? 解得V = 1m/s
（3）斜面长度L = V2/2a = 2.5m
本题解析：
本题难度：一般