时间:2019-12-13 02:37:51
1、选择题 如图所示,两根平行光滑导轨竖直放置,相距L=0.1 m,处于垂直轨道平面的匀强磁场中,磁感应强度B=10 T,质量m=0.1 kg、电阻为R=2 Ω的金属杆ab接在两导轨间,在开关S断开时让ab自由下落,ab下落过程中、始终保持与导轨垂直并与之接触良好,设导轨足够长且电阻不计,取g=10 m/s2,当下落h=0.8 m时,开关S闭合.若从开关S闭合时开始计时,则ab下滑的速度v随时间t变化的图象是图中的( )

参考答案:D.
本题解析:开关S闭合时,金属杆的速度v==4 m/s.感应电动势E=BLv,感应电流I=E/R,安培力F=BLI,联立解出F=2 N.因为F>mg=1 N,故ab杆做减速直线运动,速度减小,安培力也减小,加速度越来越小,最后加速度减为零时做匀速运动,故D正确.
本题难度:一般
2、填空题 法拉第发现了电磁感应现象之后,又发明了世界上第一台发电机──法拉第圆盘发电机,揭开了人类将机械能转化为电能并进行应用的序幕。法拉第圆盘发电机的原理如图所示,将一个圆形金属盘放置在电磁铁的两个磁极之间,并使盘面与磁感线垂直,盘的边缘附近和中心分别装有与金属盘接触良好的电刷A、B,两电刷与灵敏电流计相连。当金属盘绕中心轴按图示方向转动时,则电刷A的电势?电刷B的电势(填高于、低于或等于);若仅提高金属盘转速,灵敏电流计的示数将?;(填增大、减小或不变);若仅将滑动变阻器滑动头向左滑,灵敏电流计的示数将?(填增大、减小或不变)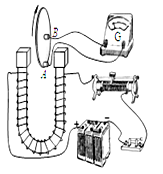
参考答案:低于?增大?减小
本题解析:根据右手定则可知电磁铁左端为N极,结合右手定则,电流从A流至B,电源内部,电流从低电势流至高电势,所以A电势低于B电势。提高转速,根据E=BLv,可知灵敏电流计的示数增大。滑动变阻器向左滑动,电阻增大,磁感应强度减小,灵敏电流计的示数减小。
本题难度:一般
3、选择题 如图甲所示,一闭合线圈固定在垂直于纸面的匀强磁场中,且线圈平面与磁场垂直。设垂直纸面向里为磁感应强度B的正方向,磁感应强度B随时间而变化的情况如图乙所示,图甲中线圈上的箭头的方向为感应电流 I的正方向。则在图中给出的线圈中感应电流I随时间而变化的图象可能正确的是( )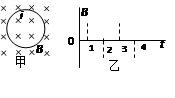
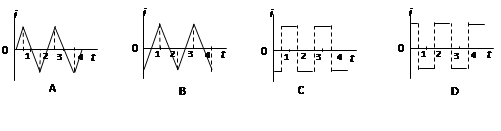
参考答案:C
本题解析:由乙图知,在0-0.5s内磁感应强度均匀增大,根据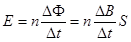 知,产生感应电动势不变,所以感应电流不变,可判断A、B错误;在0-0.5s内,B增大,磁通量
知,产生感应电动势不变,所以感应电流不变,可判断A、B错误;在0-0.5s内,B增大,磁通量 增大,根据楞次定律知感应电流的磁场与原磁场方向相反,垂直纸面向外,再由右手定则可判断感应电流方向为逆时针方向,为负,故C正确;D错误。
增大,根据楞次定律知感应电流的磁场与原磁场方向相反,垂直纸面向外,再由右手定则可判断感应电流方向为逆时针方向,为负,故C正确;D错误。
考点:本题考查法拉第电磁感应定律
本题难度:一般
4、选择题 如图甲所示线圈的匝数n=100匝,横截面积S=50cm2,线圈总电阻r=10Ω,沿轴向有匀强磁场,设图示磁场方向为正,磁场的磁感应强度随时间作如图乙所示变化,则在开始的0.1s内
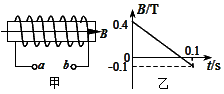
[? ]
参考答案:BD
本题解析:
本题难度:一般
5、选择题 如图1-10-7,同一水平面上足够长的固定平行导轨MN、PQ位于垂直于纸面向里的匀强磁场中,导轨上有两根金属棒ab、cd,能沿导轨无摩擦滑动,金属棒和导轨间接触良好,开始ab、cd都静止。现给cd一个向右的初速度v0,则下列说法中正确的是(?)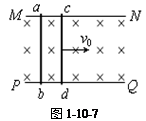 ?
?
参考答案:D
本题解析:给cd一个向右的初速度v0,则切割磁感线产生感应电流,受到向左的安培力作用,做减速运动,同时ab棒受到向右的安培力加速运动,当ab棒向右加速运动时也产生感应电动势,最终当两棒速度相等时,电路中电流为零,做匀速运动,D正确
本题难度:一般