时间:2019-12-13 02:25:58
1、计算题 如图所示,螺线管横截面积为S,线圈匝数为N,电阻为R1,管内有水平向左的变化磁场。螺线管与足够长的平行金属导轨MN、PQ相连并固定在同一平面内,与水平面的夹角为q,两导轨间距为L。导轨电阻忽略不计。导轨处于垂直斜面向上、磁感应强度为B0的匀强磁场中。金属杆ab垂直导轨,杆与导轨接触良好,并可沿导轨无摩擦滑动。已知金属杆ab的质量为m,电阻为R2,重力加速度为g。忽略螺线管磁场对金属杆ab的影响、忽略空气阻力。
(1)为使ab杆保持静止,求通过ab的电流的大小和方向;
(2)当ab杆保持静止时,求螺线管内磁场的磁感应强度B的变化率;
(3)若螺线管内方向向左的磁场的磁感应强度的变化率DB/Dt=k(k>0)。将金属杆ab由静止释放,杆将沿斜面向下运动。求当杆的速度为v时,杆的加速度大小。
参考答案:(1)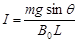 ,电流方向为由b到a(2)
,电流方向为由b到a(2)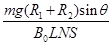 (3)
(3)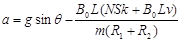
本题解析:(1)以金属杆ab为研究对象,根据平衡条件?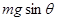 - B0I L=0(1分)
- B0I L=0(1分)
得 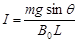 ?(1分)
?(1分)
通过ab杆电流方向为由b到a(或在图中标出)?(1分)
(2)根据法拉第电磁感应定律 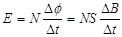 (1分)
(1分)
根据欧姆定律?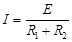 ?(1分)
?(1分)
得: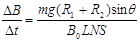 ?(1分)
?(1分)
(3)根据法拉第电磁感应定律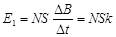 ?(1分)
?(1分)
ab杆切割磁感线产生的电动势 E2 = B0Lv?(1分)
总电动势? E总 = E1 + E2
感应电流?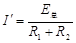 ?(1分)
?(1分)
根据牛顿第二定律?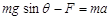 ?(1分)
?(1分)
安培力? F = B0 I′L?(1分)
所以?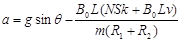 ?(1分)
?(1分)
本题难度:一般
2、选择题 动物园的水平地面上放着一只质量为M的笼子,笼内有一只质量为m的猴子.当猴子以某一加速度沿竖直柱子加速向上爬时,笼子对地面的压力为F1;当猴子以同样大小的加速度沿竖直柱子加速下滑时,笼子对地面的压力为F2,如图所示,关于F1和F2的大小,下列判断中正确的是:( )
A.F1>(M+m)g,F2<(M+m)g
B.F1=F2>(M+m)g
C.F1>F2>(M+m)g
D.F1<(M+m)g,F2>(M+m)g
参考答案:猴子在加速向上爬时对猴子分析有:猴子受到向下的重力G和向上的摩擦力f,且重力G<f,由牛顿第三定律可知笼子受到向下的摩擦力(因为笼子给猴子向上的摩擦力,所以猴子就给笼子向下的摩擦力),所以笼子给地面的压力为:F1=Mg+f,因为f>G 所以F1=Mg+f>Mg+mg
猴子在加速下滑时对猴子分析有:猴子受到向下的重力G和向上的摩擦力f,且重力G>f,由牛顿第三定律可知笼子受到向下的摩擦力(因为笼子给猴子向上的摩擦力,所以猴子就给笼子向下的摩擦力),所以笼子给地面的压力为F2=Mg+f,因为f<G? 所以F2=Mg+f<Mg+mg.A正确.
故选A
本题解析:
本题难度:一般
3、选择题 “快乐向前冲”节目中有这样一种项目,选手需要借助悬挂在高处的?绳飞跃到鸿沟对面的平台上,如果已知选手的质量为m,选手抓住绳由静止开始摆动,此时绳与竖直方向夹角为α,如图所示,不考虑空气阻力和绳的质量,下列说法正确的是( )
A.选手摆动最低点时所受绳子的拉力等于mg
B.选手摆到最低点时所受绳子的拉力为大于mg
C.选手摆到最低点时所受绳子的拉力大于选手对绳子的拉力
D.选手摆到最低点的运动过程中,其运动可分解为水平方向的匀加速运动和竖直方向上的匀加速运动
参考答案:A、B、在最低点,受到的重力和拉力的合力提供向心力,根据牛顿第二定律,有F-mg=mv2r,故F>mg,故A错误,B正确;
C、选手摆到最低点时所受绳子的拉力和选手对绳子的拉力是作用力和反作用力的关系,根据牛顿第三定律,它们大小相等、方向相反且作用在同一条直线上,故C错误;
D、选手摆到最低点的运动过程中机械能守恒,是变速圆周运动,拉力是变力,故D错误;
故选B.
本题解析:
本题难度:一般
4、选择题 如图所示,质量为m的物体,在与水平方向成θ角的拉力F作用下,在水平面上做加速度为a的匀加速运动。已知物体与水平面间有弹力作用且动摩擦因数为μ,则物体所受的各力产生的加速度的大小,下面说法正确的是
[? ]
A.滑动摩擦力产生的加速度小于μg
B.拉力F产生的加速度为
C.重力和支持力的合力产生的加速度为零
D.合力产生的加速度为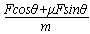 -μg
-μg
参考答案:AD
本题解析:
本题难度:一般
5、简答题 如图,有一半径为R=0.3m的光滑半圆形细管AB,将其固定在竖直墙面并使B端切线水平.一个可视为质点的质量为0.5Kg的小物体m由细管上端沿A点切线方向进入细管,从B点以速度VB=4.0m/s飞出后,恰好能从一倾角为θ=37°的倾斜传送带顶端C无碰撞的滑上传送带.已知传送带长度为L=2.75m(图中只画出了传送带的部分示意图),物体与传送带之间的动摩擦因数为u=0.50,(取sin37°=0.60,cos37°=0.80,g=10m/s2,不计空气阻力,不考虑半圆形管AB的内径).
(1)求物体在A点时的速度大小及对轨道的压力大小和方向;
(2)若传送带以V1=2.5m/s顺时针匀速转动,求物体从C到底端的过程中,由于摩擦而产生的热量Q.
参考答案:
(1)物体从A到B过程,根据机械能守恒定律得
? mg?2R=12mv2B-12mv2A?
得:vA=2m/s
设物体在A点所受轨道作用力为FA,
则由mg+FA=mv2AR,可得:FA=53N=1.67N;
由牛顿第三定律得:物体在A点时对轨道的压力大小为1.67N,方向为:竖直向上?
(2)物体落到传送带顶端C时的速度大小为:
? vC=vBcosθ=5m/s
传送带顺时针匀速转动时,对物体施加的摩擦力沿传送带表面向上
则由牛顿第二定律得
? mg(sinθ-μcosθ)=ma,
可得物体匀加速运动的加速度大小为:a=2m/s2
由L=vCt+12a1t2,得物体从C到底端的时间:t=0.5s
在此过程中,传送带相对地位移大小为s带=v1t
由于摩擦而产生的热量为Q=f?(L+s带)=μmgcosθ?(L+v1t)=8J
答:(1)物体在A点时的速度大小是2m/s,对轨道的压力大小为1.67N,方向为竖直向上;?
? (2)若传送带以V1=2.5m/s顺时针匀速转动,求物体从C到底端的过程中,由于摩擦而产生的热量Q=8J.
本题解析:
本题难度:一般