时间:2019-12-13 02:04:54
1、选择题 下列说法正确的是( )
A.两个相互接触的物体间一定存在弹力
B.将物体竖直向上抛出,物体在上升阶段所受的重力比落向地面时小
C.放在桌子上的书受到桌子对它的支持力,这是因为书发生了微小的弹性形变而产生的
D.实心球体的重心不一定在球心处
2、实验题 在用落体法验证机械能守恒定律的实验中:
( 1 )所用重锤的质量m=1.0kg,打点计时器所用电源频率50Hz,打下的纸带如右图所示(图中的数据为从起始点O到该点的距离),则 在打B点时,重锤的速度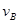 =_____________m/s,重锤的动能
=_____________m/s,重锤的动能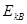 =___________J,从开始下落到打B点时,重锤的势能减小量
=___________J,从开始下落到打B点时,重锤的势能减小量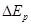 =_________J(取两位有效数字).
=_________J(取两位有效数字).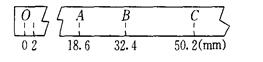
( 2 )根据纸带算出各点的速度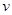 ,量出下落距离h,则以
,量出下落距离h,则以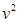 为纵轴,以h为横轴,画出的图线应是下图所示中的哪个(?)
为纵轴,以h为横轴,画出的图线应是下图所示中的哪个(?)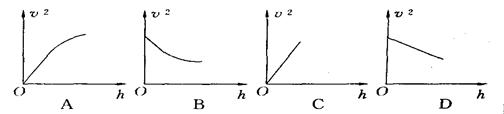
(3)根据实验所得数据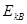 和
和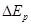 可以得到的结论是:?。
可以得到的结论是:?。
3、填空题 光电计时器是一种常用计时仪器,其结构如图所示,a、b分别是光电门的激光发射和接收装置,当有滑块从a、b间通过时,光电计时器就可以显示物体的挡光时间.现有某滑块通过光电门,计时器显示的挡光时间是5×10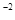 s,用最小分度值为l mm的直尺测量小滑块的长度d,示数如图所示。
s,用最小分度值为l mm的直尺测量小滑块的长度d,示数如图所示。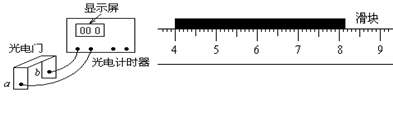
(1)读出滑块的长度d=____________cm
(2)滑块通过光电门的速度v=__________m/s
4、填空题 建筑、桥梁工程中所用的金属材料(如钢筋钢梁等)在外力作用下会伸长,其伸长量不仅与和拉力的大小有关,还和金属材料的横截面积有关.人们发现对同一种金属,其所受的拉力与其横截面积的比值跟金属材料的伸长量与原长的比值的比是一个常数,这个常数叫做杨氏模量.用E表示,即:E=
(
(
|

5、实验题 (12分)用如图实验装置验证m1、m2组成的系统机械能守恒。m2从高处由静止开始下落,m1上拖着的纸带打出一系列的点,对纸带上的点迹进行测量,即可验证机械能守恒定律。下图给出的是实验中获取的一条纸带:0是打下的第一个点,每相邻两计数点间还有4个点(图中未标出),计数点间的距离如图所示。已知m1=50g、m2=150g,则(g取10m/s2,结果保留两位有效数字)
⑴若图中用的是电火花打点计时器,则应使用(? )
A.4~6V直流电源和复写纸
B.4~6V交流电源和墨粉纸
C.220V直流电源和复写纸
D.220V交流电源和墨粉纸
⑵在打点0~5过程中系统动能的增量ΔEk=?J,系统势能的减小量ΔEp=?J,由此得出的结论是?;
⑶若某同学作出 -h图象如图,可求出当地的重力加速度g=?m/s2。
-h图象如图,可求出当地的重力加速度g=?m/s2。